题目内容
已知正方体ABCD-A1B1C1D1，平面BB1C1C内到直线AA1和直线BC距离相等的点的轨迹是（ ）
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
考点：轨迹方程
专题：圆锥曲线的定义、性质与方程
分析：如图所示，设P（x，y，0），过点P作PM⊥y轴，垂足为M，则|PM|=|x|．过点P作PE⊥AA1，PF⊥x轴，垂足分别为E，F．可得|PE|=
．由题意可得：|x|=
，即可得出．
| 1+y2 |
| 1+y2 |
解答：
解：如图所示，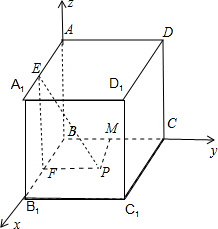
设P（x，y，0），过点P作PM⊥y轴，垂足为M，则|PM|=|x|．
过点P作PE⊥AA1，PF⊥x轴，垂足分别为E，F．
则|PE|=
．
由题意可得：|x|=
，
化为x2-y2=1．
因此满足条件的点P的轨迹是双曲线．
故选：C．
设P（x，y，0），过点P作PM⊥y轴，垂足为M，则|PM|=|x|．
过点P作PE⊥AA1，PF⊥x轴，垂足分别为E，F．
则|PE|=
| 1+y2 |
由题意可得：|x|=
| 1+y2 |
化为x2-y2=1．
因此满足条件的点P的轨迹是双曲线．
故选：C．
点评：本题考查了线面面面垂直的性质、勾股定理、双曲线的定义及其标准方程，考查了推理能力与计算能力，属于中档题．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
下列方程的曲线不关于x轴对称的是（ ）
| A、x2-x+y2=1 |
| B、x2y+xy2=1 |
| C、2x2-y2=1 |
| D、x+y2=-1 |
若命题P（n）对n=3成立，且由P（k）成立可以推证P（k+2）也成立，则一定有（ ）
| A、P（n）对所有正整数都成立 |
| B、P（n）对所有正偶数都成立 |
| C、P（n）对所有正奇数都成立 |
| D、P（n）对所有大于等于3的正奇数都成立 |
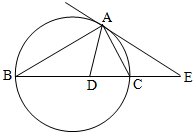如图，△ABC的外接圆的切线AE与BC的延长线交于点E，∠BAC的平分线与BC交于点D．