题目内容
设数列{an}的首项为3,数列{bn}为等差数列,且bn=an+1-an(n∈N*),若b2=-4,b9=10,则数列{an}的通项公式为an= .
考点:数列递推式
专题:等差数列与等比数列
分析:首先利用等差数列求出数列bn=2n-8,根据bn=an+1-an的特点,进一步利用叠加法求数列
{an}的通项公式.
{an}的通项公式.
解答:
解:数列{bn}为等差数列,b2=-4,b9=10,
设首相为b1,公差为d,
则:
,
解得:d=2,b1=-6,
所以:bn=2n-8,
由于:bn=an+1-an,
则:an-an-1=2(n-1)-8,
an-1-an-2=2(n-2)-8,
…
a2-a1=2•1-8,
所以:利用叠加法求得:an-a1=2(1+2+…+n-1)-8n,
解得:an=n2-9n+3,
故答案为:n2-9n+3.
设首相为b1,公差为d,
则:
|
解得:d=2,b1=-6,
所以:bn=2n-8,
由于:bn=an+1-an,
则:an-an-1=2(n-1)-8,
an-1-an-2=2(n-2)-8,
…
a2-a1=2•1-8,
所以:利用叠加法求得:an-a1=2(1+2+…+n-1)-8n,
解得:an=n2-9n+3,
故答案为:n2-9n+3.
点评:本题考查的知识要点:等差数列通项公式的应用,叠加法在数列求通项公式中的应用.属于基础题型.

练习册系列答案
相关题目
用反证法证明命题:若p则q.其第一步是反设命题的结论不成立,这个正确的反设是( )
| A、若p,则¬q | B、若¬p,则q |
| C、¬p | D、¬q |
已知正方体ABCD-A1B1C1D1,平面BB1C1C内到直线AA1和直线BC距离相等的点的轨迹是( )
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
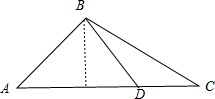 如图,一个三角形的绿地ABC,AB边的长为7m,由C点看AB的张角为45°,在AC边上一点D处看AB的张角为60°,且AD=2DC,试求这块绿地的面积.
如图,一个三角形的绿地ABC,AB边的长为7m,由C点看AB的张角为45°,在AC边上一点D处看AB的张角为60°,且AD=2DC,试求这块绿地的面积.