题目内容
6.设x,y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥0\\ 2x+y≤2\end{array}\right.$,目标函数z=ax+by(a>0,b>0)的最大值为M,若M的取值范围是[1,2],则点M(a,b)所经过的区域面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合分类求得最优解,把最优解的坐标代入目标函数,结合目标函数最大值的范围可得点M(a,b)的坐标所满足的关系式,进一步作差可行域,由梯形面积公式求解.
解答 解:由约束条件$\left\{\begin{array}{l}x≥0\\ y≥0\\ 2x+y≤2\end{array}\right.$作出可行域如图,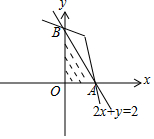
A(1,0),B(0,2),
化目标函数z=ax+by为y=$-\frac{a}{b}x+\frac{z}{b}$.
由图可知,当$-\frac{a}{b}≤-2$,即a≥2b时,目标函数的最大值a∈[1,2],此时有$\left\{\begin{array}{l}{a≥2b}\\{1≤a≤2}\\{b>0}\end{array}\right.$①;
当-$\frac{a}{b}>-2$,即a<2b时,目标函数的最大值2b∈[1,2],此时有$\left\{\begin{array}{l}{a<2b}\\{\frac{1}{2}≤b≤1}\\{a>0}\end{array}\right.$ ②.
作出①②表示的平面区域如图,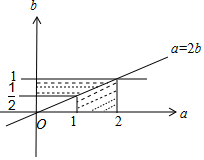
∴阴影部分的面积为$\frac{1}{2}(\frac{1}{2}+1)×1+\frac{1}{2}(1+2)×\frac{1}{2}=\frac{3}{2}$.
故选:B.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,考查数学转化思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 执行如图程序,输出的结果S=( )
执行如图程序,输出的结果S=( )
 执行如图程序,输出的结果S=( )
执行如图程序,输出的结果S=( )| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
14.已知i为虚数单位,复数z满足z(1-i)=3+2i,则z=( )
| A. | $\frac{1}{2}$+$\frac{5i}{2}$ | B. | -$\frac{1}{2}$-$\frac{5i}{2}$ | C. | $\frac{5}{2}$+$\frac{5i}{2}$ | D. | -$\frac{5}{2}$-$\frac{5i}{2}$ |
11.已知复数z=$\frac{a+i}{2i}$(其中i为虚数单位)的虚部与实部相等,则实数a的值为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | -1 | D. | $-\frac{1}{2}$ |
10.函数f(x)的定义域为R,若f(x+1)与f(x-1)都是奇函数,则f(5)=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 5 |
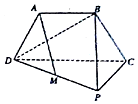 如图,三角形PCD所在的平面与等腰梯形ABCD所在的平面垂直,AB=AD=$\frac{1}{2}$CD,AB∥CD,CP⊥CD,M为PD的中点.
如图,三角形PCD所在的平面与等腰梯形ABCD所在的平面垂直,AB=AD=$\frac{1}{2}$CD,AB∥CD,CP⊥CD,M为PD的中点.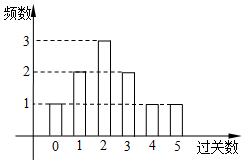 某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.