题目内容
设M={a2},N={1,4},则“a=-2”是“M⊆N”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据集合的关系以及充分条件和必要条件的定义进行判断即可.
解答:
解:∵M={a2},N={1,4},
∴若M⊆N,则a2=1或4,
即a=±1或±2,
∴“a=-2”是“M⊆N”的充分不必要条件.
故选:A.
∴若M⊆N,则a2=1或4,
即a=±1或±2,
∴“a=-2”是“M⊆N”的充分不必要条件.
故选:A.
点评:本题主要考查充分条件和必要条件的应用,利用集合的关系是解决本题的关键.

练习册系列答案
相关题目
不等式(x-2)(2x+1)>0的解集是( )
A、(-
| ||
B、(-2,
| ||
C、(-∞,-2)∪(
| ||
D、(-∞,-
|
已知α是第三象限角,其终边上一点P(x,2sin
),且cosα=
x,则
sinα+tanα=( )
| 19π |
| 6 |
| ||
| 5 |
| 5 |
| A、1 | ||
B、
| ||
C、-
| ||
| D、-1 |
函数y=sin(x-
)在区间[0,
]上( )
| π |
| 4 |
| π |
| 2 |
| A、单调递增且有最大值 |
| B、单调递增但无最大值 |
| C、单调递减且有最大值 |
| D、单调递减但无最大值 |
函数y=sin(2x-
)的单调递增区间是( )
| π |
| 3 |
A、[kπ-
| ||||
B、[2kπ-
| ||||
C、[kπ-
| ||||
D、[2kπ-
|
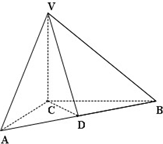 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D为AB的中点,且AC=BC=VC=a.
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D为AB的中点,且AC=BC=VC=a. 函数y=Asin(ωx+ϕ)在一个周期内的图象如图,则此函数的解析式为
函数y=Asin(ωx+ϕ)在一个周期内的图象如图,则此函数的解析式为