题目内容

函数y=sin(2x-
π
3
)的单调递增区间是（　　）
A、[kπ-
π
12
，kπ+
5π
12
]  k∈Z
B、[2kπ-
π
12
，2kπ+
5π
12
]  k∈Z
C、[kπ-
π
6
，kπ+
5π
6
]  k∈Z
D、[2kπ-
π
6
，2kπ+
5π
6
]  k∈Z
考点：正弦函数的图象
专题：三角函数的图像与性质
分析：根据正弦函数的单调性即可得到函数的增区间．
解答： 解：由-
π
2
+2kπ≤2x-
π
3
≤
π
2
+2kπ，
即-
π
6
+2kπ≤2x≤
5π
6
+2kπ，
∴-
π
12
+kπ≤x≤
5π
12
+kπ，k∈Z，
即函数的单调递增区间为：[-
π
12
+kπ，
5π
12
+kπ]，k∈Z，
故选：A．
点评：本题主要考查三角函数的单调性的判断，要求熟练掌握正弦函数的单调性，比较基础．
练习册系列答案
相关题目
设M={a2}，N={1，4}，则“a=-2”是“M⊆N”的（　　）
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要条件
将函数y=sin(2x+
π
4
)的图象向左平移
π
4
个单位，再向上平移2个单位，则所得函数的表达式是（　　）
A、y=sin(2x-
π
4
)+2
B、y=cos(2x+
π
4
)+2
C、y=sin(2x+
π
4
)-2
D、y=cos(2x-
π
4
)-2
已知tanα=-
1
2
，则sin2α-2cos2α-1=（　　）
A、-
17
5
B、-
17
4
C、-
16
5
D、-2
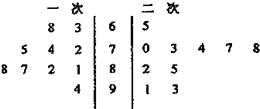如图是某同学一学期两次考试成绩的茎叶图，现从该同学两次考试成绩中各取一科成绩，则这两科成绩都在80分以上的概率为（　　）
A、
9
10
B、
3
5
C、
3
10
D、
1
5
如果曲线y=x3+x-10的切线斜率为4，求切点坐标和切线方程．
已知中心在原点的椭圆C1经过点A(
5
3
，2)，且F（0，2）是它的一个焦点．抛物线C2的顶点在原点，焦点为F（0，2），过点B（4，4）作直线交抛物线C2于M，N两点，C2在M，N两点处的切线分别是l1，l2，且l1∩l2=P．
（1）求椭圆C1的方程及它的准线方程．
（2）探究点P能否在椭圆C1上，若能，求出它的坐标，若不能说明理由．
（3）利用定积分的知识求椭圆C1的面积．
已知抛物线的顶点在坐标原点O，对称轴为x轴，焦点为F，抛物线上一点A的横坐标为2，且
FA
•
OA
=16．
（Ⅰ）求抛物线的方程；
（Ⅱ）过点M（8，0）作直线l交抛物线于B，C两点，求证：OB⊥OC．
计算：
1
2
lg25+lg2-log39=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网