题目内容
8.求直线y=-$\sqrt{3}$(x-2)绕点(2,0)按逆时针方向旋转30°所得的直线方程.分析 由题意可得已知直线的倾斜角,进而可得要求直线的倾斜角,可得斜率,可得直线方程.
解答 解:∵直线y=-$\sqrt{3}$(x-2)的斜率为-$\sqrt{3}$,倾斜角为120°,
∴直线y=-$\sqrt{3}$(x-2)绕点(2,0)按逆时针方向旋转30°所得的直线倾斜角为150°,
∴直线的斜率k=tan150°=-$\frac{\sqrt{3}}{3}$,故直线方程为y-0=-$\frac{\sqrt{3}}{3}$(x-2),
整理为一般式可得x+$\sqrt{3}$y-2=0
点评 本题考查两直线的夹角,涉及直线的倾斜角和斜率的关系,属基础题.

练习册系列答案
相关题目
19.设f(z)=$\overline{z}$,且z1=1+5i,z2=-3+2i.则f$\overline{({z}_{1}-{z}_{2})}$的值是( )
| A. | -2+3i | B. | -2-3i | C. | 4-3i | D. | 4+3i |
13.已知M(x,y)是以A(-2,3),B(3,2)为端点的线段上一动点,则$\frac{y-1}{x+1}$的取值范围为( )
| A. | [-2,$\frac{1}{4}$] | B. | (-∞,-2] | C. | (-∞,2]∪[$\frac{1}{4}$,+∞) | D. | [$\frac{1}{4}$,+∞) |
17.已知$\overrightarrow a=(cosx,-2),\overrightarrow b=(sinx,1)$且$\overrightarrow a$∥$\overrightarrow b$,则sin2x=( )
| A. | $-\frac{4}{5}$ | B. | -3 | C. | 3 | D. | $\frac{4}{5}$ |
18.在平面直角坐标系中,一束光线从点M(-2,3)出发,被直线y=x-1反射后到达点N(1,6),则这束光线从M到N所经过的路程为( )
| A. | 10$\sqrt{3}$ | B. | 3$\sqrt{10}$ | C. | 2$\sqrt{10}$ | D. | 3$\sqrt{2}$ |

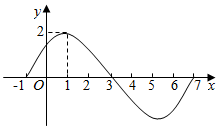 下图为函数y=Asin(ωx+φ)的一段图象,已知A>0,ω>0,φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).
下图为函数y=Asin(ωx+φ)的一段图象,已知A>0,ω>0,φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).