题目内容
己知甲、乙、丙、丁等同学竞选班委,现有4个竞选职位:班长、学习委员、纪律委员和体育委员,每个职位只需一人担任;(结果都用数字作答)
(1)问一共有多少种不同的结果?
(2)若已知甲同学担任体育委员,而乙同学没有选上,则有多少种不同的结果?
(3)若已知甲、丙两同学都当选,则有多少种不同的结果?
(1)问一共有多少种不同的结果?
(2)若已知甲同学担任体育委员,而乙同学没有选上,则有多少种不同的结果?
(3)若已知甲、丙两同学都当选,则有多少种不同的结果?
考点:排列、组合及简单计数问题
专题:应用题,排列组合
分析:(1)甲、乙、丙、丁等同学竞选班委,有4个竞选职位,利用全排列可得结论;
(2)已知甲同学担任体育委员,而乙同学没有选上,利用全排列可得结论;
(3)利用全排列可得结论.
(2)已知甲同学担任体育委员,而乙同学没有选上,利用全排列可得结论;
(3)利用全排列可得结论.
解答:
解:(1)由题意,共有
=24种不同的结果;
(2)甲同学担任体育委员,而乙同学没有选上,共有
=6种不同的结果;
(3)已知甲、丙两同学都当选,共有
=24种不同的结果.
| A | 4 4 |
(2)甲同学担任体育委员,而乙同学没有选上,共有
| A | 3 3 |
(3)已知甲、丙两同学都当选,共有
| A | 4 4 |
点评:本题考查排列、组合及简单计数问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=xlnx,则其在点(e,f(e))处的切线方程是( )
| A、y=2x-e | B、y=e |
| C、y=x-e | D、y=x+e |
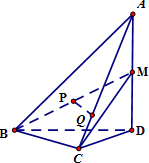 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.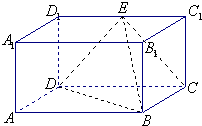 长方体ABCD-A1B1C1D1的侧棱AA1=a,AB=2a,AA1=BC=a的矩形,E为C1D1的中点.
长方体ABCD-A1B1C1D1的侧棱AA1=a,AB=2a,AA1=BC=a的矩形,E为C1D1的中点.