Question

12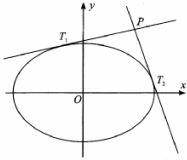．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的短轴长为2，离心率$\frac{\sqrt{2}}{2}$．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）T₁，T₂为椭圆上不同两点，过T₁，T₂作椭圆切线交于点P，若T₁P⊥T₂P，求点P的轨迹E的方程；
（Ⅲ）若PT₁交E于Q₁，PT₂交E与Q₂，求△PQ₁Q₂面积的最大值．

Answer 1

分析 （Ⅰ）运用椭圆的离心率公式和a，b，c的关系，解方程可得a，b，进而得到椭圆方程；
（Ⅱ）设P（m，n），切线的方程为y-n=k（x-m），代入椭圆方程，运用判别式为0，结合两直线垂直的条件：斜率之积为-1，化简可得P的轨迹方程；
（Ⅲ）由题意可得Q₁Q₂为圆的直径，设∠PQ₁Q₂=α，即有PQ₁=2$\sqrt{3}$cosα，PQ₂=2$\sqrt{3}$sinα，运用三角函数的二倍角公式和正弦函数的值域，即可得到所求最大值．

解答 解：（Ⅰ）由题意可得2b=2，即b=1，
e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$，a²-c²=1，
解得a=$\sqrt{2}$，b=1，
即有椭圆的方程为$\frac{{x}^{2}}{2}$+y²=1；
（Ⅱ）设P（x₀，y₀），切线的方程为y-y₀=k（x-x₀），
可得y=kx+（y₀-kx₀），
代入椭圆方程x²+2y²=2，
即有（1+2k²）x²+4k（y₀-kx₀）x+2（y₀-kx₀）²-2=0，
由直线与椭圆相切，可得△=0，
即为16k²（y₀-kx₀）²-8（1+2k²）[（y₀-kx₀）²-1]=0，
化为k²（x₀²-2）-2kx₀y₀+y₀²-1=0，
由T₁P⊥T₂P，可得k₁k₂=-1，
即有$\frac{{x}_{0}^{2}-1}{{y}_{0}^{2}-2}$=-1，
化为x₀²+y₀²=3，
可得点P的轨迹E的方程为圆x²+y²=3；
（Ⅲ）PT₁交E于Q₁，PT₂交E与Q₂，可得
Q₁Q₂为圆的直径，
设∠PQ₁Q₂=α，即有PQ₁=2$\sqrt{3}$cosα，PQ₂=2$\sqrt{3}$sinα，
则△PQ₁Q₂面积为S=$\frac{1}{2}$PQ₁•PQ₂=$\frac{1}{2}$•2$\sqrt{3}$cosα•2$\sqrt{3}$sinα
=6sinαcosα=3sin2α，
当α=45°时，sin2α取得最大值1，
即有△PQ₁Q₂面积的最大值为3．

点评 本题考查椭圆的方程的求法，注意运用离心率公式，考查直线和椭圆相切的条件：判别式为0，考查三角形的面积的最值的求法，注意运用三角函数的性质，考查化简整理的能力，属于中档题．