题目内容
3.函数f(x)=2sin(2x-$\frac{π}{3}$)在区间[0,$\frac{π}{4}$]上的最小值为( )| A. | -1 | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $-\sqrt{3}$ | D. | 1 |
分析 由条件利用正弦函数的定义域和值域,求得函数f(x)=2sin(2x-$\frac{π}{3}$)在区间[0,$\frac{π}{4}$]上的最小值.
解答 解:在区间[0,$\frac{π}{4}$]上,2x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{π}{6}$],
故函数f(x)=2sin(2x-$\frac{π}{3}$)在区间[0,$\frac{π}{4}$]上单调递增,
故当2x-$\frac{π}{3}$=-$\frac{π}{3}$时,函数取得最小值为2sin(-$\frac{π}{3}$)=-2sin$\frac{π}{3}$=-$\sqrt{3}$,
故选:C.
点评 本题主要考查正弦函数的定义域和值域,正弦函数的单调性,属于基础题.

练习册系列答案
相关题目
13.以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角形”.

该表由若干行数字组成,第一行共有2016个数字,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )

该表由若干行数字组成,第一行共有2016个数字,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )
| A. | 2016×22015 | B. | 2016×22014 | C. | 2017×22015 | D. | 2017×22014 |
14.下列说法正确的是( )
| A. | 长度相等的向量叫相等向量 | |
| B. | 零向量的长度为零 | |
| C. | 共线向量是在一条直线上的向量 | |
| D. | 平行向量就是向量所在的直线平行的向量 |
11.sin75°(sin40°cos35°+cos40°cos55°)=( )
| A. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | C. | $\frac{2+\sqrt{3}}{4}$ | D. | $\frac{2-\sqrt{3}}{4}$ |
18.若f(x)是定义在(-1,1)上的减函数,则下列不等式正确的是( )
| A. | f(sinx)>f(cosx) | B. | f($\frac{{x}^{2}+1}{2}$)>f(x) | ||
| C. | f($\frac{1}{{3}^{x}+1}$)≥f($\frac{1}{{2}^{x}+1}$) | D. | f($\frac{1}{{3}^{x}+{3}^{-x}}$)≥f($\frac{1}{{2}^{x}+{2}^{-x}}$) |
13.成等差数列的三个正数的和等于6,并且这三个数分别加上3、6、13后成为等比数列{bn}中的b3、b4、b5,则数列{bn}的通项公式为( )
| A. | bn=2n-1 | B. | bn=3n-1 | C. | bn=2n-2 | D. | bn=3n-2 |
 如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD.
如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD.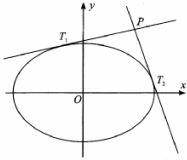 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的短轴长为2,离心率$\frac{\sqrt{2}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的短轴长为2,离心率$\frac{\sqrt{2}}{2}$.