题目内容
2.(x2+x+2y)5的展开式中,x5y2的系数为120.分析 利用二项式展开式的通项公式,即可得出结论.
解答 解:(x2+x+2y)5展开式的通项为
Tr+1=${C}_{5}^{r}$•(x2+x)5-r•(2y)r,
令r=2,则(x2+x)3的通项为:
Tk+1=${C}_{3}^{k}$•x2(3-k)•xk=${C}_{3}^{k}$•x6-k,
令6-k=5,则k=1;
所以(x2+x+2y)5的展开式中,
x5y2的系数为${C}_{5}^{2}$•22•${C}_{3}^{1}$=120.
故答案为:120.
点评 本题考查了二项式展开式通项公式的灵活应用问题,是基础题目.

练习册系列答案
相关题目
13.成等差数列的三个正数的和等于6,并且这三个数分别加上3、6、13后成为等比数列{bn}中的b3、b4、b5,则数列{bn}的通项公式为( )
| A. | bn=2n-1 | B. | bn=3n-1 | C. | bn=2n-2 | D. | bn=3n-2 |
10.设Sn是等差数列{an}的前n项和,若a1=-16,公差为2.那么使Sn取得最小值的n等于( )
| A. | 8 | B. | 8或9 | C. | 9或10 | D. | 7 |
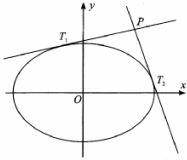 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的短轴长为2,离心率$\frac{\sqrt{2}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的短轴长为2,离心率$\frac{\sqrt{2}}{2}$.