在△ABC中.已知a=2.c=$\sqrt{3}$.B=30°.求b及A．题目和参考答案——青夏教育精英家教网—

题目内容

20．在△ABC中，已知a=2，c=$\sqrt{3}$，B=30°，求b及A．

分析利用余弦定理、正弦定理，即可得出结论．

解答解：∵△ABC中，a=2，c=$\sqrt{3}$，B=30°，
∴b=$\sqrt{4+3-2×2×\sqrt{3}×\frac{\sqrt{3}}{2}}$=1，
∵$\frac{a}{sinA}$=$\frac{b}{sinB}$，
∴sinA=$\frac{asinB}{b}$=1，
∴A=90°．

点评本题考查余弦定理、正弦定理的运用，比较基础．

练习册系列答案

期末优选卷系列答案

绿色互动空间阶梯调研测试系列答案

课本配套练习系列答案

应用题天天练东北师范大学出版社系列答案

应用题天天练四川大学出版社系列答案

全国中考试题分类精选系列答案

初中学业考试指导系列答案

练习册吉林出版集团有限责任公司系列答案

相关题目

-$\frac{\sqrt{3}}{2}$

D．

$\frac{\sqrt{3}}{2}$

11．sin75°（sin40°cos35°+cos40°cos55°）=（　　）

A．

$\frac{\sqrt{6}-\sqrt{2}}{2}$

B．

$\frac{\sqrt{6}+\sqrt{2}}{2}$

C．

$\frac{2+\sqrt{3}}{4}$

D．

$\frac{2-\sqrt{3}}{4}$

8．已知函数f（x）=ax²+|x-2a|，其中a＞0
（1）当a=1时，求f（x）在[0，+∞）上的最小值；
（2）若函数g（x）=f（x）-b在[0，+∞）上有两个零点，求实数b的取值范围（用a表示）．

15．

如图所示，AF、DE分别是⊙O、⊙O₁的直径，AD与两圆所在的平面均垂直，AD=8，BC是⊙O的直径，AB=AC=6，OE∥AD．
（1）证明：EF∥面BCD；
（2）证明：面ACD⊥面CEF；
（3）求三棱锥O₁-OBF的体积．

5．已知α、β∈（0，$\frac{π}{2}$）且sin（α+2β）=$\frac{1}{3}$．若α+β=$\frac{2π}{3}$，求sinβ的值．

12．

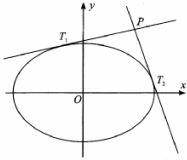已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的短轴长为2，离心率$\frac{\sqrt{2}}{2}$．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）T₁，T₂为椭圆上不同两点，过T₁，T₂作椭圆切线交于点P，若T₁P⊥T₂P，求点P的轨迹E的方程；
（Ⅲ）若PT₁交E于Q₁，PT₂交E与Q₂，求△PQ₁Q₂面积的最大值．

9．

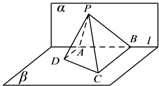如图，已知平面α⊥β，α∩β=l，A，B是直线l上的两点，C、D是平面β内的两点，且DA⊥l，CB⊥l，AD=3，AB=6，CB=6，P是平面α上的一动点，且直线PD，PC与平面α所成角相等，则二面角P-BC-D的余弦值的最小值是$\frac{\sqrt{3}}{2}$．

10．设S_n是等差数列{a_n}的前n项和，若a₁=-16，公差为2．那么使S_n取得最小值的n等于（　　）