题目内容
4.当x∈[0,2]时,函数f(x)=ax2+4(a-1)x-3在x=2时取得最大值,则实数a的取值范围是[$\frac{2}{3}$,+∞).分析 分a>0,a=0,a<0三种情况进行讨论,然后根据x的范围结合图象进行求解.
解答 解:对称轴为x=$\frac{2-2a}{a}$,
1)当a>0时,
要使x=2时候取得最大值,则 $\frac{2-2a}{a}$≤1,解得a≥$\frac{2}{3}$,
2)当a=0时,f(x)=-4x-3,x=0时候取得最大值,不符合题意,
3)当a<0时,要使x=2时候取得最大值,则 $\frac{2-2a}{a}$≥2,a≥$\frac{1}{2}$,与a<0相悖.
综上所述a的取值范围为[$\frac{2}{3}$,+∞).
故答案为:[$\frac{2}{3}$,+∞).
点评 本题考查二次函数的图象和性质,解题时要注意分类讨论思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列说法正确的是( )
| A. | 长度相等的向量叫相等向量 | |
| B. | 零向量的长度为零 | |
| C. | 共线向量是在一条直线上的向量 | |
| D. | 平行向量就是向量所在的直线平行的向量 |
13.成等差数列的三个正数的和等于6,并且这三个数分别加上3、6、13后成为等比数列{bn}中的b3、b4、b5,则数列{bn}的通项公式为( )
| A. | bn=2n-1 | B. | bn=3n-1 | C. | bn=2n-2 | D. | bn=3n-2 |
 如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD.
如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD.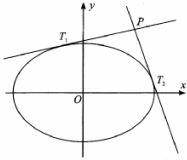 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的短轴长为2,离心率$\frac{\sqrt{2}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的短轴长为2,离心率$\frac{\sqrt{2}}{2}$.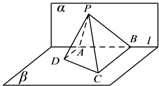 如图,已知平面α⊥β,α∩β=l,A,B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,AD=3,AB=6,CB=6,P是平面α上的一动点,且直线PD,PC与平面α所成角相等,则二面角P-BC-D的余弦值的最小值是$\frac{\sqrt{3}}{2}$.
如图,已知平面α⊥β,α∩β=l,A,B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,AD=3,AB=6,CB=6,P是平面α上的一动点,且直线PD,PC与平面α所成角相等,则二面角P-BC-D的余弦值的最小值是$\frac{\sqrt{3}}{2}$.