��Ŀ����
2��ij����ѧԺΪ�˺����й���ͳ����ʳ�Ļ����ٰ���һ������Уѧ���μӵij��մ�������ί��Ϊ���˽Ȿ�δ�������ѧ���ijɼ�������Ӳ���ѧ���г�ȡ��n��ѧ���ijɼ�������100�֣���Ϊ���������������������������������۷ֲ�ֱ��ͼ�;�Ҷͼ�����о�Ҷͼ�յ���Ⱦ����ݴ˽���������⣺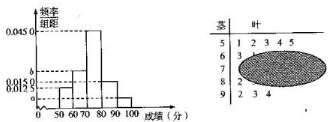
��1����Ƶ�ʷֲ�ֱ��ͼ��a��b��ֵ�����ƴ˴βμӳ��մ���ѧ����ƽ���ɼ���
��2���涨�����ɼ���[80��90����ѧ��Ϊ���ԣ���[90��100]��ѧ��Ϊ�����ִӱ���Ϊ���ԡ������ѧ���������ȡ3�ˣ����г�������ΪX����X�ķֲ�������ѧ������
���� ��1�����ȸ��ݵ�һ����ص����ݿ����n��ֵ��Ȼ�����Ƶ��=������������a�����е����֮��Ϊ1�������b��
����ƽ����=Ƶ�ʷֲ�ֱ��ͼ��ÿ�����ε��������С���εױ��е�ĺ�����֮�ͣ�
��2�����������������������������Ȼ�����ùŵ���ʹ�ʽ��������
��� �⣺�������֪��������n=$\frac{5}{0.0125��10}$=40��
��a=$\frac{3}{40��10}$=0.0075��
������С���ε�����ܺ�Ϊ1��
��0.0075+0.0125+0.0150+b+0.0450����10=1��
��b=0.0200��
�μӳ��մ���ѧ����ƽ���ɼ���0.55��0.125+65��0.2+75��0.45+85��0.15+95��0.075=73.5��
��2���������֪��������0.0150��10��40=6�ˣ�������0.0075��10��40=3��
X��ȡֵΪ��0��1��2��3��
P��X=0��=$\frac{{C}_{6}^{3}}{{C}_{9}^{3}}$=$\frac{5}{21}$��
P��X=1��=$\frac{{C}_{6}^{2}•{C}_{3}^{1}}{{C}_{9}^{3}}$=$\frac{15}{28}$��
P��X=2��=$\frac{{C}_{6}^{1}•{C}_{3}^{2}}{{C}_{9}^{3}}$=$\frac{3}{14}$��
P��X=3��=$\frac{{C}_{3}^{3}}{{C}_{9}^{3}}$=$\frac{1}{84}$��
X�ķֲ��У�
| X | 0 | 1 | 2 | 3 |
| P | $\frac{5}{21}$ | $\frac{15}{28}$ | $\frac{3}{14}$ | $\frac{1}{84}$ |
����ѧ����E��X��=1��
���� ������Ҫ����Ƶ�ʷֲ�ֱ��ͼ����Ҷͼ���ŵ���͵Ļ���֪ʶ�����ڿ������ݴ���������������������������е��⣮


�ñ���������������ɣ���һ�й���2016�����֣��ӵڶ�����ÿһ���е����־������䡰���ϡ�����֮�ͣ��������һ�н���һ�������������Ϊ��������
| A�� | 2016��22015 | B�� | 2016��22014 | C�� | 2017��22015 | D�� | 2017��22014 |
| A�� | -$\frac{1}{2}$ | B�� | $\frac{1}{2}$ | C�� | -$\frac{\sqrt{3}}{2}$ | D�� | $\frac{\sqrt{3}}{2}$ |
| A�� | ������ȵ�������������� | |
| B�� | �������ij����� | |
| C�� | ������������һ��ֱ���ϵ����� | |
| D�� | ƽ�����������������ڵ�ֱ��ƽ�е����� |
| A�� | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | B�� | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | C�� | $\frac{2+\sqrt{3}}{4}$ | D�� | $\frac{2-\sqrt{3}}{4}$ |
 ��ͼ��ABΪԲO��ֱ����PA��ֱԲO���ڵ�ƽ�棬��CΪԲO�ϵ�һ�㣮
��ͼ��ABΪԲO��ֱ����PA��ֱԲO���ڵ�ƽ�棬��CΪԲO�ϵ�һ�㣮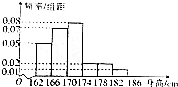 2016��߿���������У�ij�й���40000�������μ���죬�������һ��Ϊ�������ߣ�ͳ�Ƶ���������ʾ�������������߷�����̬�ֲ�N��170��16����ͳ����Ա����һ�и����IJμ����������������ȡ��50���������߲�������������ȫ������162cm��186cm֮�䣬�����������ݷֳ�6�飺��һ��[162��166�����ڶ���[166��170��������������[182��186����Ȼ���������鷽ʽ���Ƶõ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
2016��߿���������У�ij�й���40000�������μ���죬�������һ��Ϊ�������ߣ�ͳ�Ƶ���������ʾ�������������߷�����̬�ֲ�N��170��16����ͳ����Ա����һ�и����IJμ����������������ȡ��50���������߲�������������ȫ������162cm��186cm֮�䣬�����������ݷֳ�6�飺��һ��[162��166�����ڶ���[166��170��������������[182��186����Ȼ���������鷽ʽ���Ƶõ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��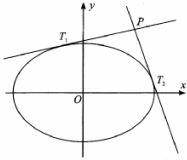 ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1�Ķ��᳤Ϊ2��������$\frac{\sqrt{2}}{2}$��
��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1�Ķ��᳤Ϊ2��������$\frac{\sqrt{2}}{2}$��