题目内容
设x,y∈R,则“x≥2,且y≥2”是“x2+y2≥8”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:若“x≥2,且y≥2”,则“x2+y2≥8”;反之不成立,如取x=0,y=3.即可判断出.
解答:
解:若“x≥2,且y≥2”,则“x2+y2≥8”;
反之不成立,如取x=0,y=3.
因此“x≥2,且y≥2”是“x2+y2≥8”的充分不必要条件.
故选:A.
反之不成立,如取x=0,y=3.
因此“x≥2,且y≥2”是“x2+y2≥8”的充分不必要条件.
故选:A.
点评:本题考查了充分必要条件的判定,考查了推理能力,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
若函数f(x)=Asin(ωx+φ)+1(ω>0,|φ|<π)对任意实数t,都有f(t+
)=f(-t+
),记g(x)=Acos(ωx+φ)-1,则g(
)=( )
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
曲线y=
在点(0,0)处的切线方程为( )
| x |
| x+2 |
| A、y=2x | ||
| B、y=2x-2 | ||
C、y=
| ||
D、y=
|
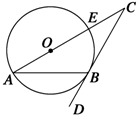 如图所示,CD切⊙O于B,CO的延长线交⊙O于A,若∠C=36°,则∠ABD的度数是( )
如图所示,CD切⊙O于B,CO的延长线交⊙O于A,若∠C=36°,则∠ABD的度数是( )| A、72° | B、63° |
| C、54° | D、36° |
已知在△ABC中,BC=6,AB=4,cosB=
,则AC=( )
| 1 |
| 3 |
| A、6 | ||
B、2
| ||
C、3
| ||
D、4
|
已知函数f(x),当自变量x由x0增加到x0+△x时,函数值的增量与自变量的增量的比值为( )
| A、函数在x0处的变化率 |
| B、函数在区间[x0,x0+△x]上的平均变化率 |
| C、函数在x0+△x处的变化率 |
| D、函数在x0处的导数 |
平行于同一条直线的两条直线间的位置关系是( )
| A、异面 | B、平行 |
| C、相交 | D、以上都有可能 |