题目内容
已知点P（a，b）与点Q（1，0）在直线2x-3y+1=0的两侧，且a＞0且a≠1，b＞0，则
的取值范围是 ．
| b |
| a-1 |
考点：直线的斜率
专题：直线与圆
分析：由点P（a，b）与点Q（1，0）在直线2x-3y+1=0的两侧，可得（2a-3b+1）（2+1）＜0，即2a+1＜3b．又a＞0且a≠1，b＞0，画出可行域．
=
表示可行域内的点（a，b）与点P（1，0）的斜率k．即可得出．
| b |
| a-1 |
| b-0 |
| a-1 |
解答：
解：∵点P（a，b）与点Q（1，0）在直线2x-3y+1=0的两侧，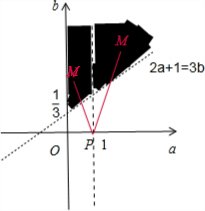
∴（2a-3b+1）（2+1）＜0，即2a+1＜3b．
又a＞0且a≠1，b＞0，画出可行域：
=
表示可行域内的点（a，b）与点P（1，0）的斜率k．
当点M经过(0，
)时，kPM=
=-
．
∴点M位于直线x=1的左侧时，k＜kPM=-
．
当点M位于直线x=1的右侧时，k＞
．
因此
的取值范围是(-∞，-
)∪(
，+∞)．
故答案是：(-∞，-
)∪(
，+∞)．
∴（2a-3b+1）（2+1）＜0，即2a+1＜3b．
又a＞0且a≠1，b＞0，画出可行域：
| b |
| a-1 |
| b-0 |
| a-1 |
当点M经过(0，
| 1 |
| 3 |
| ||
| 0-1 |
| 1 |
| 3 |
∴点M位于直线x=1的左侧时，k＜kPM=-
| 1 |
| 3 |
当点M位于直线x=1的右侧时，k＞
| 2 |
| 3 |
因此
| b |
| a-1 |
| 1 |
| 3 |
| 2 |
| 3 |
故答案是：(-∞，-
| 1 |
| 3 |
| 2 |
| 3 |
点评：本题考查了线性规划问题、直线的斜率计算公式及其单调性，考查了问题的转化能力和推理能力，属于难题．
练习册系列答案
相关题目
某市对排污水进行综合治理，征收污水处理费，系统对各厂一个月内排出的污水量m吨收取的污水处理费y元，运行程序如下所示：函数f（x）=
+cosx，x∈[0，
]的最大值是（ ）
| x |
| 2 |
| π |
| 2 |
| A、1 | ||||||
B、
| ||||||
C、
| ||||||
D、
|