Question

设O为坐标原点，抛物线C：y²=2px（p＞0）的准线为l，焦点为F，过F斜率为

3

的直线与抛物线C相交于A，B两点，直线AO与l相交于D，若|AF|＞|BF|，则

|BD|

|OF|

=

 

．

Answer 1

考点：抛物线的简单性质

专题：圆锥曲线中的最值与范围问题

分析：由题设知直线AB的方程为y=

3

（x-

p

2

），l的方程为x=-

p

2

，联立

y= 3 (x- p 2 ) y2=2px

，解得A（-

3

2

p，

3

P），B（

p

6

，-

3

3

p），直线OA的方程为：y=

2 3

3

x，联立

y= 2 3 3 x x=- p 2

，解得D（-

p

2

，-

3

3

p），由此能求出

|BD|

|OF|

．

解答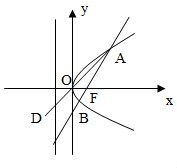： 解：∵O为坐标原点，抛物线C：y²=2px（p＞0）的准线为l，焦点为F，
过F斜率为

3

的直线与抛物线C相交于A，B两点，
直线AO与l相交于D，
∴直线AB的方程为y=

3

（x-

p

2

），l的方程为x=-

p

2

，
联立

y= 3 (x- p 2 ) y2=2px

，解得A（-

3

2

p，

3

P），B（

p

6

，-

3

3

p）
∴直线OA的方程为：y=

2 3

3

x，
联立

y= 2 3 3 x x=- p 2

，解得D（-

p

2

，-

3

3

p）
∴|BD|=

( p 6 + p 2 )2+(- 3 3 p+ 3 3 p)2

=

2

3

p，
∵|OF|=

1

2

p，∴

|BD|

|OF|

=

2 3 p

1 2 p

=

4

3

．
故答案为：

4

3

．

点评：本题考查两条件线段的比值的求法，是中档题，解题时要认真审题，要熟练掌握抛物线的简单性质．