题目内容
12.在正方体ABCD-A1B1C1D1中,M为棱A1B1的中点,则异面直线AM与B1C所成的角的大小为arccos$\frac{\sqrt{10}}{5}$(结果用反三角函数值表示).分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线AM与B1C所成的角.
解答  解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1棱长为2,
则A(2,0,0),M(2,1,2),B1(2,2,2),C(0,2,0),
$\overrightarrow{AM}$=(0,1,2),$\overrightarrow{{B}_{1}C}$=(-2,0,2),
设异面直线AM与B1C所成的角为θ,
cosθ=$\frac{|\overrightarrow{AM}•\overrightarrow{{B}_{1}C}|}{|\overrightarrow{AM}|•|\overrightarrow{{B}_{1}C}|}$=$\frac{|4|}{\sqrt{5}×\sqrt{8}}$=$\frac{\sqrt{10}}{5}$.
∴θ=$arccos\frac{\sqrt{10}}{5}$.
∴异面直线AM与B1C所成的角为arccos$\frac{\sqrt{10}}{5}$.
故答案为:$arccos\frac{{\sqrt{10}}}{5}$.
点评 本题考查异面直线所成角的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
20.设等差数列{an}满足a2=7,a4=3,Sn是数列{an}的前n项和,则使得Sn>0最大的自然数n是( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
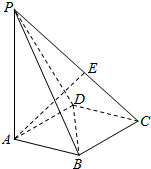 如图,底面为菱形P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AB.
如图,底面为菱形P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AB.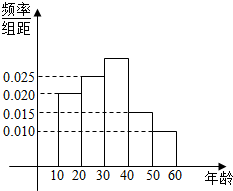 某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.
某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.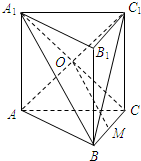 如图,已知直三棱柱ABC-A1B1C1的侧面ACC1A1是正方形,点O是侧面ACC1A1的中心,∠ACB=$\frac{π}{2}$,M是棱BC的中点.
如图,已知直三棱柱ABC-A1B1C1的侧面ACC1A1是正方形,点O是侧面ACC1A1的中心,∠ACB=$\frac{π}{2}$,M是棱BC的中点.