题目内容
2.若a∈R+,则当a+$\frac{1}{9a}$的最小值为m时,不等式m${\;}^{{x}^{2}+4x+3}$<1的解集为{x|x<-3或x>-1}.分析 利用基本不等式求出a+$\frac{1}{9a}$的最小值m,再代入不等式m${\;}^{{x}^{2}+4x+3}$<1,化为等价的不等式x2+4x+3>0,求出解集即可.
解答 解:∵a∈R+,∴a+$\frac{1}{9a}$≥2$\sqrt{a•\frac{1}{9a}}$=$\frac{2}{3}$,
当且仅当a=$\frac{1}{9a}$,即a=$\frac{1}{3}$时取“=”;
∴a+$\frac{1}{9a}$的最小值为m=$\frac{2}{3}$;
∴不等式m${\;}^{{x}^{2}+4x+3}$<1为:
($\frac{2}{3}$)${\;}^{{x}^{2}+4x+3}$<1,
等价于x2+4x+3>0,
解得x<-3或x>-1;
故所求不等式的解集为{x|x<-3或x>-1}.
故答案为:{x|x<-3或x>-1}.
点评 本题考查了利用基本不等式求最值以及指数不等式的解法与应用问题,是基础题目.

练习册系列答案
相关题目
12.已知a=$\sqrt{0.4}$,b=20.4,c=0.40.2,则a,b,c三者的大小关系是( )
| A. | b>c>a | B. | b>a>c | C. | a>b>c | D. | c>b>a |
13.下列命题中为真命题的是( )
| A. | 命题“若x>1,则x2>1”的否命题 | B. | 命题“若x>y,则x>|y|”的逆命题 | ||
| C. | 命题“若x=1,则x2+x-2=0”的否命题 | D. | 命题“若x2≥1,则x≥1”的逆否命题 |
 如图,在一个面积为8的矩形中随机撒一粒黄豆,若黄豆落到阴影部分的概率为$\frac{1}{4}$,则阴影部分的面积为2.
如图,在一个面积为8的矩形中随机撒一粒黄豆,若黄豆落到阴影部分的概率为$\frac{1}{4}$,则阴影部分的面积为2.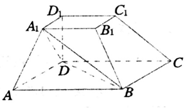 如图所示,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.
如图所示,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.