题目内容
4个不同的小球放入3个不同的盒子中（盒子不允许为空），一共有 种不同的放法．
考点：计数原理的应用
专题：排列组合
分析：根据题意，分2步进行，先要从4个球中选2个作为一个元素，再同其他的两个元素在三个位置全排列，分别求出每一步的情况数目，再根据乘法原理得到结果．
解答：
解：由题意知四个不同的小球全部随意放入三个不同的盒子中，则必须有1个盒子里放2个球，其余的三个盒子各放1个，
首先要从4个球中选2个作为一个元素，有C42种结果，
同其他的两个元素在三个位置全排列有A33种情况，
根据分步乘法原理知共有C42A33=36；
故答案为：36
首先要从4个球中选2个作为一个元素，有C42种结果，
同其他的两个元素在三个位置全排列有A33种情况，
根据分步乘法原理知共有C42A33=36；
故答案为：36
点评：本题考查排列、组合的运用，是常见的题型，要注意题意的要求，如本题中的小球、盒子是否相同．
练习册系列答案
相关题目
若m＞0，0＜n＜1，则函数y=m+lognx的图象可能是（ ）
A、 |
B、 |
C、 |
D、 |
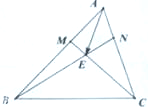在△ABC中，已知AM：AB=1：3，AN：AC=1：4，BN与CM交于点E，