题目内容
已知过点(0,1)的直线l:xtanα-y-3tanβ=0的斜率为2,则tan(α+β)= .
考点:两角和与差的正切函数
专题:三角函数的求值
分析:求出直线的斜率,得到tanα,利用点在直线上求出tanβ,利用两角和的正切函数求解即可.
解答:
解:因为直线l:xtanα-y-3tanβ=0的斜率为2,所以tanα=2.
直线化为:2x-y-3tanβ=0,点(0,1)在直线上,
所以tanβ=-
.
tan(α+β)=
=
=1
故答案为:1.
直线化为:2x-y-3tanβ=0,点(0,1)在直线上,
所以tanβ=-
| 1 |
| 3 |
tan(α+β)=
| tanα+tanβ |
| 1-tanαtanβ |
2-
| ||
1+2×
|
故答案为:1.
点评:本题考查两角和与差的三角函数,直线的斜率,考查计算能力.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
若m>0,0<n<1,则函数y=m+lognx的图象可能是( )
A、 |
B、 |
C、 |
D、 |
已知f(x)是偶函数,且x>0时,f(x)=x2+ax,若f(-1)=2,则f(2)的值是( )
| A、-1 | B、1 | C、3 | D、6 |
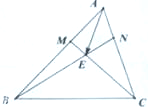 在△ABC中,已知AM:AB=1:3,AN:AC=1:4,BN与CM交于点E,
在△ABC中,已知AM:AB=1:3,AN:AC=1:4,BN与CM交于点E,