题目内容
已知cosα-sinα=
，
＜α＜
，求sin2α和tan（
+α）的值．
3
| ||
| 5 |
| 17π |
| 12 |
| 7π |
| 4 |
| π |
| 4 |
考点：二倍角的正弦,两角和与差的正切函数
专题：三角函数的求值
分析：（1）由已知cosα-sinα=
，
＜α＜
，知（sinα-cosα）2=1-sin2α=
，由此能求出sin2α．
3
| ||
| 5 |
| 17π |
| 12 |
| 7π |
| 4 |
| 18 |
| 25 |
解答：
解：因为cosα-sinα=
，平方可得 1-2sinαcosα=
，所以2sinαcosα=
，所以sin2α=
；
又
＜α＜
，故sinα+cosα＜0，所以sinα+cosα=-
=-
=-
，
tan（
+α）=
=-
=-
．
3
| ||
| 5 |
| 18 |
| 25 |
| 7 |
| 25 |
| 7 |
| 25 |
又
| 17π |
| 12 |
| 7π |
| 4 |
| (sinα+cosα)2 |
| 1+sin2α |
4
| ||
| 5 |
tan（
| π |
| 4 |
| sinα+cosα |
| cosα-sinα |
| ||||
|
| 4 |
| 3 |
点评：本题考查三角函数的化简求值，解题时要认真审题，仔细求解，注意三角函数恒等变换的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
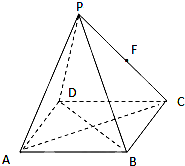如图，在四棱锥P-ABCD中，底面ABCD为正方形，且PA=PB=PC=PD，F为PC中点．