题目内容
设数列{an}满足a1=2,a2+a4=8,且对任意n∈N*,函数f(x)= (an-an+1+an+2)x+an+1·cosx-an+2·sin x满足f′
(an-an+1+an+2)x+an+1·cosx-an+2·sin x满足f′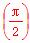 =0.
=0.
(1)求数列{an}的通项公式;
(2)若bn=2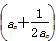 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
解析:(1)由a1=2,a2+a4=8
f(x)=(an-an+1+an+2)x+an+1·cos x-an+2·sin x,
f′(x)=an-an+1+an+2-an+1·sin x-an+2·cos x,
所以f′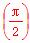 =an-an+1+an+2-an+1=0,
=an-an+1+an+2-an+1=0,
所以,2an+1=an+an+2,
所以{an}是等差数列.
而a1=2,a3=4,d=1,
an=2+ (n-1)×1=n+1(n∈N*).
(n-1)×1=n+1(n∈N*).
(2)bn=2 =2(n+1)+
=2(n+1)+ ,
,
Sn=
=n(n+3)+1- =n2+3n+1-
=n2+3n+1- .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
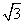 ),则|u*(u+v)|=__
),则|u*(u+v)|=__ ______.
______. 7 19
7 19 _______.
_______.
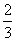 ,2);
,2);