题目内容
已知函数f(x)=x3-2x2-4x-7,其导函数为f ′(x).则以下四个命题:
①f(x)的单调减区间是(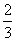 ,2);
,2);
②f(x)的极小值是-15;
③当a>2时,对任意的x>2且x≠a,恒有f(x)>f(a)+f ′(a)(x-a);
④函数f(x)有且只有一个零点.
其中真命题的个数为( )
A.1个 B.2个
C.3个 D.4个
C
[解析] f ′(x)=3x2-4x-4=(3x+2)(x-2),可得f(x)在(-∞,-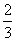 )上为增函数,在(-
)上为增函数,在(-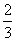 ,2)上为减函数,在(2,+∞)上为增函数,故①错误;f(x)极小值=f(2)=-15,故②正确;在(2,+∞)上,f(x)为“下凸”函数,
,2)上为减函数,在(2,+∞)上为增函数,故①错误;f(x)极小值=f(2)=-15,故②正确;在(2,+∞)上,f(x)为“下凸”函数,
又a>2,x≠a,当x>a时,有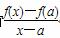 >f ′(a)恒成立;当x<a时,有
>f ′(a)恒成立;当x<a时,有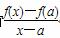 <f ′(a)恒成立,故恒有f(x)>f(a)+f ′(a)(x-a),故③正确;f(x)极大值=f(-
<f ′(a)恒成立,故恒有f(x)>f(a)+f ′(a)(x-a),故③正确;f(x)极大值=f(-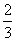 )<0,故函数f(x)只有一个零点,④正确.真命题为②③④,故选C.
)<0,故函数f(x)只有一个零点,④正确.真命题为②③④,故选C.

练习册系列答案
相关题目
 (an-an+1+an+2)x+an+1·cosx-an+2·sin x满足f′
(an-an+1+an+2)x+an+1·cosx-an+2·sin x满足f′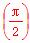 =0.
=0.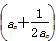 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.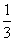 x3+
x3+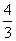 .
.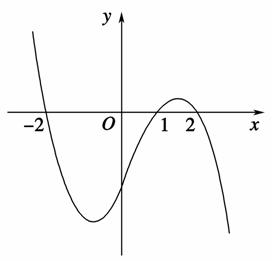
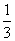 x3-
x3- ax2+(a-1)x+1在区间(1,4)上为减函数,在区间(6,+∞)上为增函数,试求实数a的取值范围.
ax2+(a-1)x+1在区间(1,4)上为减函数,在区间(6,+∞)上为增函数,试求实数a的取值范围. 在区间[1,4]上存在次不动点,则实数a的取值范围是( )
在区间[1,4]上存在次不动点,则实数a的取值范围是( ) ,则S100=________.
,则S100=________.