题目内容
实数x,y满足
,则z=x-2y的最小值为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用目标函数的几何意义,进行求最值即可.
解答:
解:由z=x-2y得y=
x-
,
作出不等式组对应的平面区域如图(阴影部分ABC):
平移直线y=
x-
,
由图象可知当直线y=
x-
,过点A时,直线y=
x-
的截距最大,此时z最小,
由
,解得
,即A(1,
).
代入目标函数z=x-2y,
得z=1-2×
=1-3=-2
∴目标函数z=x-2y的最小值是-2.
故答案为:-2
| 1 |
| 2 |
| z |
| 2 |

作出不等式组对应的平面区域如图(阴影部分ABC):
平移直线y=
| 1 |
| 2 |
| z |
| 2 |
由图象可知当直线y=
| 1 |
| 2 |
| z |
| 2 |
| 1 |
| 2 |
| z |
| 2 |
由
|
|
| 3 |
| 2 |
代入目标函数z=x-2y,
得z=1-2×
| 3 |
| 2 |
∴目标函数z=x-2y的最小值是-2.
故答案为:-2
点评:本题主要考查线性规划的基本应用,利用目标函数的几何意义是解决问题的关键,利用数形结合是解决问题的基本方法.

练习册系列答案
相关题目
某几何体的三视图如图,则该几何体的表面积为( )


A、3+
| ||
| B、6 | ||
C、3+
| ||
D、2+
|
 某几何体是由直三棱柱与圆锥的组合体,起直观图和三视图
某几何体是由直三棱柱与圆锥的组合体,起直观图和三视图如图所示,正视图为正方形,其中俯视图中椭圆的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
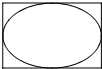 如图所示,矩形长为3,宽为2,在矩形内随机撒200颗黄豆,数得落在椭圆内的黄豆数为160颗,依据此实验数据可以估计出椭圆的面积约为( )
如图所示,矩形长为3,宽为2,在矩形内随机撒200颗黄豆,数得落在椭圆内的黄豆数为160颗,依据此实验数据可以估计出椭圆的面积约为( )| A、4.7 | B、4.8 |
| C、1.2 | D、1.3 |
若双曲线
-
=1(a>0,b>0)的渐近线与圆(x-2)2+y2=1有公共点,则此双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||||
B、(1,
| ||||
C、(
| ||||
D、[
|
过双曲线
-
=1的右焦点的直线交双曲线的右支于A,B两点,设F是双曲线的左焦点,e是双曲线的离心率,若△ABF为等腰三角形,且∠A=90°,则e2=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、4-2
| ||
B、5-2
| ||
C、6-2
| ||
D、7-2
|
按如图所示的程序框图,若输出的结果为170,则判断框内应填入的条件为( )


| A、i≥5 | B、i≥7 |
| C、i≥9 | D、i≥11 |
关于空间两条直线a、b和平面α,下列命题正确的是( )
| A、若a∥b,b?α,则a∥α |
| B、若a∥α,b?α,则a∥b |
| C、若a⊥α,b⊥α,则a∥b |
| D、若a∥α,b∥α,则a∥b |