题目内容
在△ABC中，证明：
=
．
| a |
| sinA |
| a+b |
| sinA+sinB |
考点：正弦定理的应用
专题：证明题,解三角形
分析：由正弦定理
=
=
=2r，（r为△ABC的外接圆的半径）可得a=2rsinA，b=2rsinB，代入即可得证．
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
解答：
证明：由正弦定理
=
=
=2r，（r为△ABC的外接圆的半径）
可得a=2rsinA，b=2rsinB，
则
=
=2r=
，
则
=
．
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
可得a=2rsinA，b=2rsinB，
则
| a+b |
| sinA+sinB |
| 2rsinA+2rsinB |
| sinA+sinB |
| a |
| sinA |
则
| a |
| sinA |
| a+b |
| sinA+sinB |
点评：本题考查正弦定理的运用，考查运算能力，属于基础题．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
已知向量
与
的夹角为30°，且|
|=1，|2
-
|=1，则|
|=（ ）
| a |
| b |
| a |
| a |
| b |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
某几何体是由直三棱柱与圆锥的组合体，起直观图和三视图如图所示，正视图为正方形，其中俯视图中椭圆的离心率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
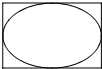如图所示，矩形长为3，宽为2，在矩形内随机撒200颗黄豆，数得落在椭圆内的黄豆数为160颗，依据此实验数据可以估计出椭圆的面积约为（ ）| A、4.7 | B、4.8 |
| C、1.2 | D、1.3 |