题目内容
设函数f(x)=2sinxcos2
+cosxsinφ-sinx(0<φ<π)在x=π处取最小值.
(1)求φ的值;
(2)若实数α满足f(α)+f(
-α)=
,α∈(
,π),试求
的值.
| φ |
| 2 |
(1)求φ的值;
(2)若实数α满足f(α)+f(
| π |
| 2 |
| 1 |
| 5 |
| π |
| 2 |
| sin2α+cos2α-1 |
| sinα-cosα |
考点:三角函数中的恒等变换应用
专题:三角函数的求值,三角函数的图像与性质
分析:(1)首先,化简函数解析式,得到f(x)=sin(x+φ),然后,根据函数f(x)在x=π处取最小值,确定φ=
;
(2)根据(1),得到f(x)=cosx,然后,根据f(α)+f(
-α)=
,得到sinα+cosα=
,从而得到sinα-cosα=
,最后,化简
=-2sinα,从而确定其值.
| π |
| 2 |
(2)根据(1),得到f(x)=cosx,然后,根据f(α)+f(
| π |
| 2 |
| 1 |
| 5 |
| 1 |
| 5 |
| 7 |
| 5 |
| sin2α+cos2α-1 |
| sinα-cosα |
解答:
解:(1)∵f(x)=2sinxcos2
+cosxsinφ-sinx,
∴f(x)=2sinx•
+cosxsinφ-sinx
=sinx+sinxcosφ+cosxsinφ-sinx
=sin(x+φ),
∴f(x)=sin(x+φ),
∵函数f(x)在x=π处取最小值.
且0<φ<π,
∴φ=
.
(2)根据(1)得
f(x)=sin(x+
)=cosx,
∴f(α)+f(
-α)
=cosα+cos(
-α)=
,
∴sinα+cosα=
,
∵
=
=
=-2sinα
∵sinα+cosα=
,且α∈(
,π),
∴sinα-cosα=
,
∴sinα=
,
∴
的值为-
.
| φ |
| 2 |
∴f(x)=2sinx•
| 1+cosφ |
| 2 |
=sinx+sinxcosφ+cosxsinφ-sinx
=sin(x+φ),
∴f(x)=sin(x+φ),
∵函数f(x)在x=π处取最小值.
且0<φ<π,
∴φ=
| π |
| 2 |
(2)根据(1)得
f(x)=sin(x+
| π |
| 2 |
∴f(α)+f(
| π |
| 2 |
=cosα+cos(
| π |
| 2 |
| 1 |
| 5 |
∴sinα+cosα=
| 1 |
| 5 |
∵
| sin2α+cos2α-1 |
| sinα-cosα |
=
| 2sinαcosα-2sin2α |
| sinα-cosα |
=
| 2sinα(cosα-sinα) |
| sinα-cosα |
=-2sinα
∵sinα+cosα=
| 1 |
| 5 |
| π |
| 2 |
∴sinα-cosα=
| 7 |
| 5 |
∴sinα=
| 4 |
| 5 |
∴
| sin2α+cos2α-1 |
| sinα-cosα |
| 8 |
| 5 |
点评:本题重点考查了三角函数的图象与性质、三角公式等知识,属于中档题.

练习册系列答案
相关题目
执行如图的程序框图,输出的结果为( )
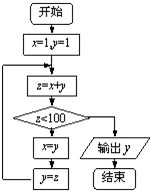

| A、55 | B、89 |
| C、144 | D、233 |
到原点的距离等于4的动点的轨迹方程是( )
| A、x2+y2=4 |
| B、x2+y2=16 |
| C、x2+y2=2 |
| D、(x-4)2+(y-4)2=16 |
命题“如果实数x能被2整除,则x是偶数”的否命题是( )
| A、如果实数x不能被2整除,则x是偶数 |
| B、如果实数x能被2整除,则x不是偶数 |
| C、如果实数x不能被2整除,则x不是偶数 |
| D、存在一个能被2整除的数,它不是偶数 |
设全集为U,若存在D1与D2(D1≠D2),D1⊆U,D2⊆U,使得y=f(x),x∈D1与y=f(x),x∈D2的值域相同,则称这两个函数为一对“同族函数“.现在U=[0,2π),f(x)=sinx,值域为[
,
]的“同族函数“共有( )对.
| 1 |
| 2 |
| ||
| 2 |
| A、6对 | B、15对 |
| C、36对 | D、1对 |
已知全集U=R,M={x|x>1},N={x|x≤-1,或x≥5},则M∩(∁UN)=( )
| A、{x|1<x≤5} |
| B、{x|1<x<5} |
| C、{x|-1<x<5} |
| D、∅ |