题目内容
设f（x）是定义在R上的奇函数，且f（-2）=0，当x＞0时，有
＞0恒成立，则不等式xf（x）＞0的解集是（ ）
| xf′(x)-f(x) |
| x2 |
| A、（-2，0）∪（2，+∞） |
| B、（-2，0）∪（0，2） |
| C、（-∞，-2）∪（0，2） |
| D、（-∞，-2）∪（2，+∞） |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：首先构造函数g（x）=
，然后得到该函数的单调区间，最后结合该函数的取值情形，进行求解．
| f(x) |
| x |
解答：
解：∵
＞0（x＞0），
设函数g（x）=
，
∴g′（x）=
＞0，
∴g（x）的单调递增区间为（0，+∞），
∵g（-x）=
=
=g（x），
∴g（x）为偶函数，
∴g（x）的单调递减区间为（-∞，0），
∵f（-2）=0，
∴g（-2）=0．g（2）=0，
∴当x＜-2时，g（x）＞0，
当-2＜x＜0时，g（x）＜0，
当0＜x＜2时，g（x）＜0，
当x＞2时，g（x）＞0，
∵不等式xf（x）＞0的解集等价于g（x）＞0，
∴当x＜-2或x＞2时，g（x）＞0，
不等式xf（x）＞0的解集{x|x＜-2或x＞2}．
故选：D．
| xf′(x)-f(x) |
| x2 |
设函数g（x）=
| f(x) |
| x |
∴g′（x）=
| xf′(x)-f(x) |
| x2 |
∴g（x）的单调递增区间为（0，+∞），
∵g（-x）=
| f(-x) |
| -x |
| -f(x) |
| -x |
∴g（x）为偶函数，
∴g（x）的单调递减区间为（-∞，0），
∵f（-2）=0，
∴g（-2）=0．g（2）=0，
∴当x＜-2时，g（x）＞0，
当-2＜x＜0时，g（x）＜0，
当0＜x＜2时，g（x）＜0，
当x＞2时，g（x）＞0，
∵不等式xf（x）＞0的解集等价于g（x）＞0，
∴当x＜-2或x＞2时，g（x）＞0，
不等式xf（x）＞0的解集{x|x＜-2或x＞2}．
故选：D．
点评：题重点考查了函数的基本性质，函数的单调性与导数之间的关系等知识点，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
三个人独立地破译一个密码，他们能单独译出的概率分别为
，
，
，假设他们破译密码是彼此独立的，则此密码被破译出的概率为（ ）
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
| D、不确定 |
已知函数f（x）对任意x，y∈R，总有f（x）+f（y）=f（x+y），且当x＞0时，f（x）＜0，f（1）=-
．
（1）求证：f（x）在R上是减函数．
（2）求函数在[-3，3]上的最大值和最小值．
| 2 |
| 3 |
（1）求证：f（x）在R上是减函数．
（2）求函数在[-3，3]上的最大值和最小值．
如图，△ABC内接于⊙O，AB是⊙O的不是直径的弦，∠CAD=∠ABC，判断直线AD与⊙O的位置关系，并说明理由．
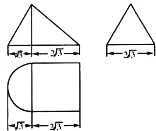一个几何体的三视图如图所示，且其左视图是一个等边三角形，则这个几何体的体积为（ ）A、12+
| ||
B、36+
| ||
C、18+
| ||
D、6+
|