题目内容
在空间四边形ABCD中,M,N分别为 BC,CD的中点,O为BD的中点,且AB=BC=CD=DA,求证:MN⊥平面AOC.
考点:直线与平面垂直的判定
专题:空间位置关系与距离
分析:利用三角形中位线性质,得到MN∥BD,只要再判断BD与平面AOC垂直即可.
解答:
 证明:如图
证明:如图
因为M,N分别为 BC,CD的中点,
所以MN∥BD,
因为O为BD的中点,且AB=BC=CD=DA,
所以BD⊥OA,BD⊥OC,
所以BD⊥平面AOC,
所以MN⊥平面AOC.
 证明:如图
证明:如图因为M,N分别为 BC,CD的中点,
所以MN∥BD,
因为O为BD的中点,且AB=BC=CD=DA,
所以BD⊥OA,BD⊥OC,
所以BD⊥平面AOC,
所以MN⊥平面AOC.
点评:本题考查了线面垂直的判定定理的运用,熟练线面垂直的判定定理是关键,属于基础题;

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
设函数f(x)=
(a>0a≠1),其中[m]表示不超过m的最大整数,如[4.1]=4,则函数y=[f(x)-
]+[f(-x)-
]的值域是( )
| ax |
| 1+ax |
| 1 |
| 2 |
| 1 |
| 2 |
| A、{0,1} |
| B、{-1,1} |
| C、{-1,0} |
| D、{-1,0,1} |
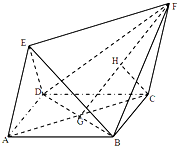 如图,四边形ABCD为菱形,ACFE为平行四边形,且面ACFE⊥面ABCD,AB=BD=2,AE=
如图,四边形ABCD为菱形,ACFE为平行四边形,且面ACFE⊥面ABCD,AB=BD=2,AE=