题目内容
已知椭圆
+
=1(a>b>0)的左右焦点为F1、F2,且过点P(3,4),若PF1⊥PF2,则椭圆方程为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:椭圆过点P(3,4),且PF1⊥PF2,可得
+
=1,
×
=-1,又a2=b2+c2.解出即可.
| 9 |
| a2 |
| 16 |
| b2 |
| 4 |
| 3+c |
| 4 |
| 3-c |
解答:
解:∵椭圆过点P(3,4),且PF1⊥PF2,
∴
+
=1,
×
=-1,又a2=b2+c2.
联立解得a2=45,b2=20,c2=25.
∴椭圆的标准方程为:
+
=1.
故答案为
+
=1.
∴
| 9 |
| a2 |
| 16 |
| b2 |
| 4 |
| 3+c |
| 4 |
| 3-c |
联立解得a2=45,b2=20,c2=25.
∴椭圆的标准方程为:
| x2 |
| 45 |
| y2 |
| 20 |
故答案为
| x2 |
| 45 |
| y2 |
| 20 |
点评:本题考查了椭圆的标准方程及其性质、直线垂直与斜率的关系,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
复数
的共轭复数为( )
| 5 |
| 3+4i |
| A、3-4i | ||||
| B、3+4i | ||||
C、
| ||||
D、
|
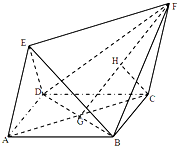 如图,四边形ABCD为菱形,ACFE为平行四边形,且面ACFE⊥面ABCD,AB=BD=2,AE=
如图,四边形ABCD为菱形,ACFE为平行四边形,且面ACFE⊥面ABCD,AB=BD=2,AE=