题目内容

已知f（x）=
2x-b
(x-1)2
无极值，则b的值为（　　）
A、1B、2C、3D、4
考点：利用导数研究函数的极值
专题：导数的综合应用
分析：先求出函数的导数，由题意可得f′（x）=0解出即可．
解答： 解：∵f′（x）=
2(x-1)-2(2x-b)
(x-1)3
=
-2(x+1-b)
(x-1)3
，
∴若函数f（x）=
2x-b
(x-1)2
无极值，则1-b=-1，∴b=2．
故选B．
点评：本题考察了函数的单调性、极值，导数的应用，是一道基础题．
练习册系列答案
相关题目
已知f（x）的定义域[1，2]，则f（x2-1）的定义域
 
．
函数f（x）在定义域R上的导函数是f′（x），若f（x）=f（2-x），且当x∈（-∞，1）时，（x-1）f′（x）＜0，设a=f（0、b=f（
2
）、c=f（log28），则（　　）
A、a＜b＜c
B、a＞b＞c
C、c＜a＜b
D、a＜c＜b
下列五个命题：
①log2x2=2log2x；
②A∪B=A的充要条件是B⊆A；
③将钟的分针拨快10分钟，则分针转过的角度是60°；
④若y=ksinx+1，x∈R，则y的最小值为-k+1；
⑤若函数f（x）=
(3a-1)x+4a(x＜1)
logax(x≥1)
对任意的x1≠x2都有
f(x2)-f(x2)
x2-x1
＜0则实数a的取值范围是（
1
7
，
1
3
）．
其中正确命题的序号为
 
（写出所有正确命题的序号）．
设f（x）=2ax-5（a＞0且a≠1）在[-1，2]上的最大值为3
（1）求a的值；
（2）当a＞1时，求f（x）在（-∞，0）上的值域．
如图，在正方体ABCD-A1B1C1D1中，E是AA1的中点，
（1）求证：A1C∥平面BDE；
（2）求三棱锥E-BCD的体积；
（3）求点E到点C1的距离|EC1|．
已知函数f（x）=alnx-x-
x2
2
，a∈R．
（Ⅰ）讨论函数f（x）的单调性；
（Ⅱ） 证明：（x-1）（e-x-x）+2lnx＜
2
3
．
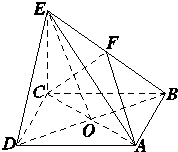如图所示，在四棱锥E-ABCD中，底面ABCD是正方形，AC与BD交于点O，EC⊥底面ABCD，F为BE的中点．
（1）求证：平面BDE⊥平面ACE；
（2）已知CE=1，点M为线段BD上的一个动点，直线EM与平面ABCD所成角的最大值为
π
4
．
①求正方形ABCD的边长；
②在线段EO上是否存在一点G，使得CG⊥平面BDE？若存在，求出
EG
EO
的值；若不存在，请说明理由．
设抛物线y2=8x上一点P到y轴距离是6，则点p到该抛物线焦点的距离是（　　）
A、12B、8C、6D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网