题目内容
已知f(x)的定义域[1,2],则f(x2-1)的定义域 .
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:要求函数的定义域,就是求函数式x2-1中x的取值范围.
解答:
解:因为函数y=f(x)的定义域是[1,2],
所以函数 f(x2-1)中1≤x2-1≤2,
∴2≤x2≤3,
即x∈[-
,-
]∪[
,
]
f(x2-1)的定义域为[-
,-
]∪[
,
]
故答案为:[-
,-
]∪[
,
]
所以函数 f(x2-1)中1≤x2-1≤2,
∴2≤x2≤3,
即x∈[-
| 3 |
| 2 |
| 2 |
| 3 |
f(x2-1)的定义域为[-
| 3 |
| 2 |
| 2 |
| 3 |
故答案为:[-
| 3 |
| 2 |
| 2 |
| 3 |
点评:本题考查函数的定义域并且是抽象函数的定义域,本题解题的关键是不管所给的是函数是什么形式只要使得括号中的部分范围一致即可.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
下列说法中,正确的是( )
| A、命题“若am2<bm2,则a<b”的逆命题是真命题 |
| B、命题“存在x0∈R,x02-x0>0”的否定是:“任意x∈R,x2-x≤0” |
| C、命题“p或q”为真命题,则命题“p”和命题“q”均为真命题 |
| D、已知m,n∈R,则“lnm<lnn”是“em<en”的必要不充分条件 |
 执行如图所示的程序框图,则输出的b值等于( )
执行如图所示的程序框图,则输出的b值等于( )| A、-3 | B、-8 |
| C、-15 | D、-24 |
函数y=ax+1+2(a>0且a≠1)图象一定过点( )
| A、(0,2) |
| B、(-1,3) |
| C、(-1,2) |
| D、(0,3) |
执行如图所示的程序框图,输出i的值为( )


| A、2 | B、3 | C、4 | D、5 |
已知f(x)=
无极值,则b的值为( )
| 2x-b |
| (x-1)2 |
| A、1 | B、2 | C、3 | D、4 |
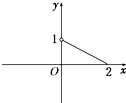 已知定义在[-2,2]上的奇函数f(x)在(0,2]上的图象如图所示,
已知定义在[-2,2]上的奇函数f(x)在(0,2]上的图象如图所示,