题目内容
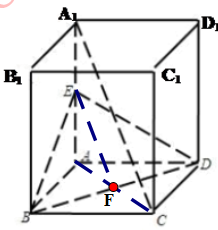
 如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点,
如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点,(1)求证:A1C∥平面BDE;
(2)求三棱锥E-BCD的体积;
(3)求点E到点C1的距离|EC1|.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)确定EF∥A1C,根据直线与平面平行的判定定理可以判断A1C∥平面BDE
(2)根据条件公式求解,(3)运用距离公式求解.
(2)根据条件公式求解,(3)运用距离公式求解.
解答:
(1)证明:连接AC交BD于点F,连接EF
由正方体ABCD-A1B1C1D1知,四边形ABCD为正方形;
 ∴F为AC中点,又已知E为AA1中点,
∴F为AC中点,又已知E为AA1中点,
则EF∥A1C,又EF⊆平面BDE∴A1C∥平面BDE
(2)分别以AB,AD,AA1为x,y,z轴建立坐标系,
得出:E(0,0,1),C1(2,2,2)
∴|EC1|=
=3
由正方体ABCD-A1B1C1D1知,四边形ABCD为正方形;
 ∴F为AC中点,又已知E为AA1中点,
∴F为AC中点,又已知E为AA1中点,则EF∥A1C,又EF⊆平面BDE∴A1C∥平面BDE
(2)分别以AB,AD,AA1为x,y,z轴建立坐标系,
得出:E(0,0,1),C1(2,2,2)
∴|EC1|=
| (2-0)2+(2-0)2+(2-1)2 |
点评:本题考察了空间直线的位置关系,求解体积距离等问题,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 执行如图所示的程序框图,则输出的b值等于( )
执行如图所示的程序框图,则输出的b值等于( )| A、-3 | B、-8 |
| C、-15 | D、-24 |
已知f(x)=
无极值,则b的值为( )
| 2x-b |
| (x-1)2 |
| A、1 | B、2 | C、3 | D、4 |
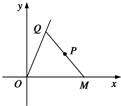 有定点P(6,4)及定直线l:y=4x,点Q是l上在第一象限内的点,PQ交x轴的正半轴于点M,
有定点P(6,4)及定直线l:y=4x,点Q是l上在第一象限内的点,PQ交x轴的正半轴于点M,
