题目内容
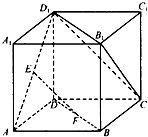 如图,已知正方体ABCD-A1B1C1D1的棱长为1,E、F分别为AD1、BD的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为1,E、F分别为AD1、BD的中点.(1)求证:EF∥平面B1D1C;
(2)求直线AD1与直线B1C所成的角,
(3)求二面角B1-D1C-A的余弦值.
考点:二面角的平面角及求法,异面直线及其所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)证明EF∥平面B1D1C,利用线面平行的判定定理,只需证明EF∥D1C;
(2)连接BC1,∵正方体ABCD-A1B1C1D1,∴BC1∥AD1,∴AD1与直线B1C所成的角即BC1与直线B1C所成的角;
(3)取D1C的中点M,连接AM,B1M,B1A,证明∠AMB1为二面角B1-D1C-A的平面角,计算用余弦定理,即可求得二面角B1-D1C-A的大小.
(2)连接BC1,∵正方体ABCD-A1B1C1D1,∴BC1∥AD1,∴AD1与直线B1C所成的角即BC1与直线B1C所成的角;
(3)取D1C的中点M,连接AM,B1M,B1A,证明∠AMB1为二面角B1-D1C-A的平面角,计算用余弦定理,即可求得二面角B1-D1C-A的大小.
解答:
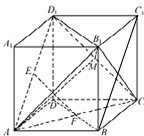 (1)证明:连接AC,在△AD1C中,
(1)证明:连接AC,在△AD1C中,
∵F为BD的中点,∴F为AC的中点
∵E为AD1的中点,
∴EF∥D1C
∵EF?平面B1D1C,D1C?平面B1D1C
∴EF∥平面B1D1C;
(2)解:连接BC1,∵正方体ABCD-A1B1C1D1,
∴BC1∥AD1,∴AD1与直线B1C所成的角即BC1与直线B1C所成的角,
∵正方形BCC1B1,∴BC1⊥B1C,∴直线AD1与直线B1C所成的角为90°.
(3)解:取D1C的中点M,连接AM,B1M,B1A
∵△AD1C为正三角形,M为CD1的中点
∴AM⊥D1C
同理,在正三角形B1D1C,B1M⊥D1C
∴∠AMB1为二面角B1-D1C-A的平面角
∵正方体ABCD-A1B1C1D1的棱长为1
∴AM=
,B1M=
,B1A=
,
∴cos∠AMB1=
.
 (1)证明:连接AC,在△AD1C中,
(1)证明:连接AC,在△AD1C中,∵F为BD的中点,∴F为AC的中点
∵E为AD1的中点,
∴EF∥D1C
∵EF?平面B1D1C,D1C?平面B1D1C
∴EF∥平面B1D1C;
(2)解:连接BC1,∵正方体ABCD-A1B1C1D1,
∴BC1∥AD1,∴AD1与直线B1C所成的角即BC1与直线B1C所成的角,
∵正方形BCC1B1,∴BC1⊥B1C,∴直线AD1与直线B1C所成的角为90°.
(3)解:取D1C的中点M,连接AM,B1M,B1A
∵△AD1C为正三角形,M为CD1的中点
∴AM⊥D1C
同理,在正三角形B1D1C,B1M⊥D1C
∴∠AMB1为二面角B1-D1C-A的平面角
∵正方体ABCD-A1B1C1D1的棱长为1
∴AM=
| ||
| 2 |
| ||
| 2 |
| 2 |
∴cos∠AMB1=
| 1 |
| 3 |
点评:本题考查线面平行,异面直线所成的角,考查面面角,解题的关键是掌握线面平行的判定定理,正确作出异面直线所成的角,面面角,属于中档题.

练习册系列答案
相关题目
一个样本容量为20的样本数据,它们组成一个等差数列{an},若a1=4,a20=42,则此样本的平均数和中位数分别是( )
| A、22,23 |
| B、23,22 |
| C、23,24 |
| D、23,23 |
若m,n是两条不同的直线,α,β,γ为三个不同的平面,则下列命题正确的是( )
| A、若m∥n,m?α,则n∥α |
| B、若m∥n,m?α,n?β,则β∥α |
| C、若α⊥γ,β⊥α,则β∥γ |
| D、若m∥n,m⊥α,n⊥β,则β∥α |
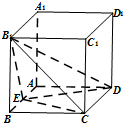 如图,正方体ABCD-A1B1C1D1中,E是AB的中点
如图,正方体ABCD-A1B1C1D1中,E是AB的中点