题目内容
某同学大学毕业后在一家公司上班,工作年限x和年收入y(万元),有以下的统计数据:
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)根据上表提供的数据,用最小二乘法求得y关于x的线性回归方程为
=0.7x+a,求a的值;
(Ⅲ)请你估计该同学第8年的年收入约是多少?
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(Ⅱ)根据上表提供的数据,用最小二乘法求得y关于x的线性回归方程为
 |
| y |
(Ⅲ)请你估计该同学第8年的年收入约是多少?
考点:回归分析
专题:应用题,概率与统计
分析:(I)以工作年限为x轴,年收入为y轴,根据表格数据,可得散点图;
(II)计算系数,即可得到线性回归方程;
(III)利用线性回归方程,可估计估计该同学第8年的年收入数.
(II)计算系数,即可得到线性回归方程;
(III)利用线性回归方程,可估计估计该同学第8年的年收入数.
解答:
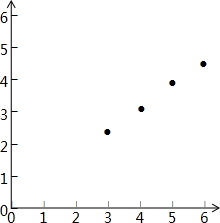 解:(Ⅰ)散点图如图.…(4分)
解:(Ⅰ)散点图如图.…(4分)
(Ⅱ)
=4.5,
=3.5,
xiyi=66.5,
xi2=86,
∴b=0.7,a=
-b
=0.35,100
∴回归直线方程为y=0.7x+0.35…(9分)
(Ⅲ)当x=8时,y=5.95
计该同学第8年的年收入约是5.95万元.…(12分)
 解:(Ⅰ)散点图如图.…(4分)
解:(Ⅰ)散点图如图.…(4分)(Ⅱ)
. |
| x |
. |
| y |
| 4 |
 |
| i=1 |
| 4 |
 |
| i=1 |
∴b=0.7,a=
. |
| y |
. |
| x |
∴回归直线方程为y=0.7x+0.35…(9分)
(Ⅲ)当x=8时,y=5.95
计该同学第8年的年收入约是5.95万元.…(12分)
点评:本题考查线性回归知识,考查学生的计算能力,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
若双曲线x2+
=1的离心率是2,则焦距为( )
| y2 |
| k |
| A、2 | ||
B、2
| ||
C、2
| ||
| D、4 |
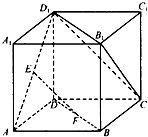 如图,已知正方体ABCD-A1B1C1D1的棱长为1,E、F分别为AD1、BD的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为1,E、F分别为AD1、BD的中点.