题目内容
已知函数f(x)=
.
(1)写出函数f(x)的对称中心;
(2)若x≥3,求f(x)的取值范围;
(3)若将f(x)的图象沿x轴水平向左平移两个单位,再向下平移一个单位,得到g(x)的图象,求出g(x)的表达式.
| x-1 |
| x-2 |
(1)写出函数f(x)的对称中心;
(2)若x≥3,求f(x)的取值范围;
(3)若将f(x)的图象沿x轴水平向左平移两个单位,再向下平移一个单位,得到g(x)的图象,求出g(x)的表达式.
考点:函数的图象与图象变化,函数的值域
专题:函数的性质及应用
分析:(1)利用分子常数化,即可写出函数f(x)的对称中心;
(2)根据分式不等式的性质,结合不等式的运算,即可求f(x)的取值范围;
(3)根据函数图象平移之间的关系即可求出g(x)的表达式.
(2)根据分式不等式的性质,结合不等式的运算,即可求f(x)的取值范围;
(3)根据函数图象平移之间的关系即可求出g(x)的表达式.
解答:
解:(1)f(x)=
=
=1+
,
则函数f(x)的对称中心为(2,1);
(2)∵f(x)=
=
=1+
在(2,+∞)上单调递减,
若x≥3,则x-2≥1,∴0<
≤1,
即1<1+
≤1+1=2,
即1<f(x)≤2,
即f(x)的取值范围(1,2];
(3)若将f(x)的图象沿x轴水平向左平移两个单位,得到y=1+
,
再向下平移一个单位,为y=
,
即g(x)=
.
| x-1 |
| x-2 |
| x-2+1 |
| x-2 |
| 1 |
| x-2 |
则函数f(x)的对称中心为(2,1);
(2)∵f(x)=
| x-1 |
| x-2 |
| x-2+1 |
| x-2 |
| 1 |
| x-2 |
若x≥3,则x-2≥1,∴0<
| 1 |
| x-2 |
即1<1+
| 1 |
| x-2 |
即1<f(x)≤2,
即f(x)的取值范围(1,2];
(3)若将f(x)的图象沿x轴水平向左平移两个单位,得到y=1+
| 1 |
| x |
再向下平移一个单位,为y=
| 1 |
| x |
即g(x)=
| 1 |
| x |
点评:本题主要考查分式函数的图象和性质,要求熟练掌握分式函数的求解方法.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
在约束条件
下,则目标函数z=4x+2y的取值范围是( )
|
| A、[0,12] |
| B、[2,10] |
| C、[0,10] |
| D、[2,12] |
在△ABC中,a=
,b=
,B=
,则A=( )
| 2 |
| 3 |
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|


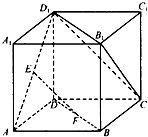 如图,已知正方体ABCD-A1B1C1D1的棱长为1,E、F分别为AD1、BD的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为1,E、F分别为AD1、BD的中点.