题目内容
9.已知函数f(x)=$\left\{\begin{array}{l}{-x^2+4x,x≤0}\\{ln(x+1),x>0}\end{array}\right.$,若函数g(x)=f(x)-mx有且只有一个零点,则实数m的取值范围是( )| A. | [1,4] | B. | (-∞,0] | C. | (-∞,4] | D. | (-∞,0]∪[1,4] |
分析 若函数g(x)=f(x)-mx有且只有一个零点,则函数f(x)与函数y=mx的图象只有一个交点,数形结合可得答案.
解答 解:若函数g(x)=f(x)-mx有且只有一个零点,
则函数f(x)与函数y=mx的图象只有一个交点,
在同在坐标系中画出两个函数的图象如下图所示: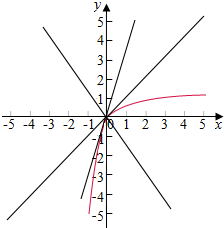
∵f′(x)=$\left\{\begin{array}{l}-2x+4,x≤0\\ \frac{1}{x+1},x>0\end{array}\right.$,
故当m∈(-∞,0]∪[1,4]时,两个函数图象有且只有一个交点,
即函数g(x)=f(x)-mx有且只有一个零点,
故选:D.
点评 本题考查的知识点是分段函数的应用,函数的零点,数形结合思想,难度中档.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
20.若函数f(x)=ln(x),则f(e-2)等于( )
| A. | -1 | B. | -2 | C. | -e | D. | -2e |
18.已知函数f(x)=$\left\{\begin{array}{l}{|lgx|,0<x≤10}\\{-\frac{x}{2}+6,x>10}\end{array}\right.$,若函数y=f2(x)-2bf(x)+b-$\frac{2}{9}$有6个零点,则b的取值范围是( )
| A. | ($\frac{2}{9}$,$\frac{1}{3}$)∪($\frac{2}{3}$,$\frac{7}{9}$) | B. | (-∞,$\frac{1}{3}$)∪($\frac{2}{3}$,+∞) | C. | (0,$\frac{1}{3}$)∪($\frac{2}{3}$,1) | D. | ($\frac{2}{9}$,$\frac{7}{9}$) |
19.有红、黄、蓝旗各3面,每次升1面、2面、3面在某一旗杆上纵向排列,共可以组成( )种不同的信号.
| A. | 27 | B. | 30 | C. | 36 | D. | 39 |