题目内容
18.已知函数f(x)=$\left\{\begin{array}{l}{|lgx|,0<x≤10}\\{-\frac{x}{2}+6,x>10}\end{array}\right.$,若函数y=f2(x)-2bf(x)+b-$\frac{2}{9}$有6个零点,则b的取值范围是( )| A. | ($\frac{2}{9}$,$\frac{1}{3}$)∪($\frac{2}{3}$,$\frac{7}{9}$) | B. | (-∞,$\frac{1}{3}$)∪($\frac{2}{3}$,+∞) | C. | (0,$\frac{1}{3}$)∪($\frac{2}{3}$,1) | D. | ($\frac{2}{9}$,$\frac{7}{9}$) |
分析 作函数f(x)=$\left\{\begin{array}{l}{|lgx|,0<x≤10}\\{-\frac{x}{2}+6,x>10}\end{array}\right.$的图象,从而化为函数y=x2-2bx+b-$\frac{2}{9}$在(0,1)上有2个零点,从而解得.
解答 解:作函数f(x)=$\left\{\begin{array}{l}{|lgx|,0<x≤10}\\{-\frac{x}{2}+6,x>10}\end{array}\right.$的图象如下,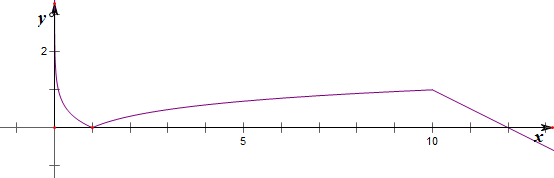 ,
,
∵函数y=f2(x)-2bf(x)+b-$\frac{2}{9}$有6个零点,
∴函数y=x2-2bx+b-$\frac{2}{9}$在(0,1)上有2个零点,
∴$\left\{\begin{array}{l}{b-\frac{2}{9}>0}\\{1-2b+b-\frac{2}{9}>0}\\{0<b<1}\\{{b}^{2}-2{b}^{2}+b-\frac{2}{9}<0}\end{array}\right.$,
解得,b∈($\frac{2}{9}$,$\frac{1}{3}$)∪($\frac{2}{3}$,$\frac{7}{9}$),
故选:A.
点评 本题考查了函数的图象的作法及数形结合的思想应用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
9.已知函数f(x)=$\left\{\begin{array}{l}{-x^2+4x,x≤0}\\{ln(x+1),x>0}\end{array}\right.$,若函数g(x)=f(x)-mx有且只有一个零点,则实数m的取值范围是( )
| A. | [1,4] | B. | (-∞,0] | C. | (-∞,4] | D. | (-∞,0]∪[1,4] |
7.若直线3x+4y+12=0和6x+8y-11=0之间的距离为一圆的直径,则此圆的面积是( )
| A. | $\frac{49}{16}$π | B. | $\frac{32}{25}$π | C. | $\frac{32}{4}$π | D. | $\frac{7}{5}$π |