题目内容
直角坐标系中,曲线C1的参数方程为
,(α为参数),M是曲线C1上的动点,点P满足
=2
,
(1)求点P的轨迹方程C2;
(2)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线θ=
与曲线C1,C2交于不同于原点的点A,B,求|AB|.
|
| OP |
| OM |
(1)求点P的轨迹方程C2;
(2)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线θ=
| π |
| 3 |
考点:点的极坐标和直角坐标的互化,参数方程化成普通方程
专题:坐标系和参数方程
分析:(1)设出P点坐标,得到M的坐标,代入曲线C1后可得点P的轨迹方程C2;
(2)求出曲线C1和C2的极坐标方程,联立射线θ=
,求得射线θ=
与曲线C1,C2交于不同于原点的点A,B的极坐标,则|AB|可求.
(2)求出曲线C1和C2的极坐标方程,联立射线θ=
| π |
| 3 |
| π |
| 3 |
解答:
解:(1)设动点P(x,y),则由
=2
得M(
,
),
∵点M在曲线C1上,
∴
,即
.
∴曲线C2的参数方程为
;
(2)曲线C1的极坐标方程为ρ=4sinθ,曲线C2的极坐标方程为ρ=8sinθ,
它们与射线θ=
交于两点A,B的极径分别是ρ1=4sin
=2
,ρ2=8sin
=4
.
∴|AB|=|ρ1-ρ2|=2
.
| OP |
| OM |
| x |
| 2 |
| y |
| 2 |
∵点M在曲线C1上,
∴
|
|
∴曲线C2的参数方程为
|
(2)曲线C1的极坐标方程为ρ=4sinθ,曲线C2的极坐标方程为ρ=8sinθ,
它们与射线θ=
| π |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 3 |
| 3 |
∴|AB|=|ρ1-ρ2|=2
| 3 |
点评:本题考查坐标系与参数方程的有关内容,求解时既可以化成直角坐标方程求解,也可以直接求解,关键是掌握两种坐标系下的曲线与方程的关系与其他知识的联系,是基础题.

练习册系列答案
相关题目
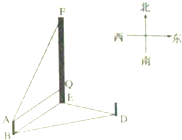 如图所示,要测量山高EF,把测量仪器放到点B处得到数据∠FAQ=75°,点E位于点B的北偏东60°方向上,从点B沿北偏东75°方向前行30m到达点D,利用仪器测得点E在点D的北偏西60°方向上,求山高EF.(已知仪器高2m)
如图所示,要测量山高EF,把测量仪器放到点B处得到数据∠FAQ=75°,点E位于点B的北偏东60°方向上,从点B沿北偏东75°方向前行30m到达点D,利用仪器测得点E在点D的北偏西60°方向上,求山高EF.(已知仪器高2m)