题目内容
13.设x,y满足约束条件$\left\{\begin{array}{l}{x+y-3≤0}\\{x-y+1≥0}\\{y≥1}\end{array}\right.$,则z=2x-y的取值范围为[-1,3].分析 由约束条件作出可行域,数形结合得到最优解,求出最优解的坐标,代入目标函数得答案
解答  解:可行域对应的区域如图:
解:可行域对应的区域如图:
当直线y=2x-z经过A时,目标函数最小,当经过B时最大;其中A(0,1),
由$\left\{\begin{array}{l}{y=1}\\{x+y=3}\end{array}\right.$得到A(2,1),
所以目标函数z=2x-y的最小值为2×0-1=-1,最大值为2×2-1=3;故目标函数z=2x-y的取值范围为[-1,3];
故答案为:[-1,3].
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
4.函数f(x)=2x2+3x+1的零点是( )
| A. | -$\frac{1}{2}$,-1 | B. | $\frac{1}{2}$,1 | C. | $\frac{1}{2}$,-1 | D. | -$\frac{1}{2}$,1 |
5.一个几何体的三视图如图所示,则该几何体的表面积为( )
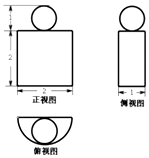

| A. | 4π+4 | B. | 2π+4 | C. | 3π | D. | 4π |
2.已知集合A={x∈R||x-1|<1},B={y∈R|y=2x+1,x∈R},则A∩(∁RB)=( )
| A. | (0,2) | B. | [1,2) | C. | (0,1] | D. | (0,1) |
3.函数y=sin(2x+$\frac{π}{6}$)的图象可看成是把函数y=sin2x的图象做以下平移得到( )
| A. | 向右平移$\frac{π}{6}$ | B. | 向左平移 $\frac{π}{12}$ | C. | 向右平移 $\frac{π}{12}$ | D. | 向左平移$\frac{π}{6}$ |
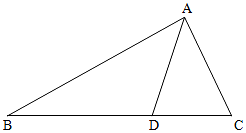 如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{\sqrt{2}}{10}$.
如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{\sqrt{2}}{10}$.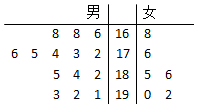 M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.