题目内容
5.一个几何体的三视图如图所示,则该几何体的表面积为( )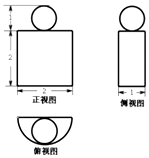
| A. | 4π+4 | B. | 2π+4 | C. | 3π | D. | 4π |
分析 根据三视图得出组合体是由半圆柱和球的组合体,算出半圆柱体与球体的表面积,求和即可.
解答 解:根据三视图知,该几何体是半圆柱体与球体的组合体;
根据图中数据知,半圆柱体的半径为1,高为2,
球体的半径为$\frac{1}{2}$;
则该几何体的表面积为
S=S半圆柱体+S球体
=(2×$\frac{1}{2}$π×12+π×1×2+2×2)+4π×${(\frac{1}{2})}^{2}$
=4π+4.
故选:A.
点评 本题考查了利用几何体三视图求表面积的应用问题,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.若集合A=$\left\{{x\left|{\frac{x}{x-1}≤0}\right.}\right\}$,B={x|x2<2x},则“x∈A∩B”是“x∈(0,1)”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
17.已知f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x>0}\\{cos2πx,x≤0}\end{array}\right.$,则f($\frac{1}{2}$)+f(-$\frac{1}{2}$)的值等于( )
| A. | 0 | B. | ±2 | C. | 2 | D. | -2 |
15.集合A={x|x2-a≤0},B={x|x<2},若A⊆B,则实数a的取值范围是( )
| A. | (-∞,4] | B. | (-∞,4) | C. | [0,4] | D. | (0,4) |
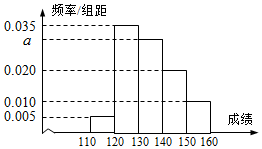 从高三年级随机抽取200名学生,将他们的某次考试数学成绩绘制成频率分布直方图.由图中数据可知成绩在[130,140)内的学生人数为60.
从高三年级随机抽取200名学生,将他们的某次考试数学成绩绘制成频率分布直方图.由图中数据可知成绩在[130,140)内的学生人数为60.