题目内容
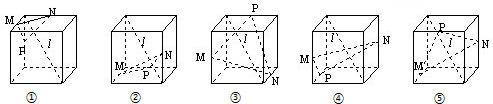
如图,下列五个正方体图形中,I是正方体的一条对角线,点M、N、P分别为其所在棱的中点,能得出I垂直于平面MNP的图形的序号是 .

考点:直线与平面垂直的判定
专题:空间位置关系与距离
分析:设定正方体的顶点如图,连结DB,AC,根据M,N分别为中点,判断出MN∥AC,由四边形ABCD为正方形,判断出AC⊥BD进而根据DD′⊥平面ABCD,AC?平面ABCD,判断出DD′⊥AC,进而根据线面垂直的判定定理推断出AC⊥平面DBB′,根据线面垂直的性质可知AC⊥DB′,利用线面垂直的判定定理推断出由MN∥AC,推断出DB′⊥MN,同理可证DB′⊥MF,DB′⊥NF,利用线面垂直的判定定理推断出DB′⊥平面MNF.④中由①中证明可知I⊥MP,根据MN∥AC,AC⊥I,推断出I⊥MN,进而根据线面垂直的判定定理推断出I⊥平面MNP,同理可证明⑤中I⊥平面MNP.
解答:
解: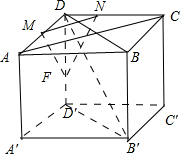 设定正方体的顶点如图,连结DB,AC,
设定正方体的顶点如图,连结DB,AC,
∵M,N分别为中点,
∴MN∥AC,
∵四边形ABCD为正方形,
∴AC⊥BD,
∵BB′⊥平面ABCD,AC?平面ABCD,
∴BB′⊥AC,
∵BB′∩DB′=B,BB′?平面DBB′,AC?平面DBB′,
∴AC⊥平面DBB′,
∵DB′?平面DBB′,
∴AC⊥DB′,
∵MN∥AC,
∴DB′⊥MN,
同理可证DB′⊥MF,DB′⊥NF,
∵MF∩NF=F,MF?平面MNF,NF?平面MNF,
∴DB′⊥平面MNF,即I垂直于平面MNP,故①正确.
④中由①中证明可知I⊥MP,
∵MN∥AC,
AC⊥I,
∴I⊥MN,
∴I⊥平面MNP,
同理可证明⑤中I⊥平面MNP.
故答案为:①④⑤
 设定正方体的顶点如图,连结DB,AC,
设定正方体的顶点如图,连结DB,AC,∵M,N分别为中点,
∴MN∥AC,
∵四边形ABCD为正方形,
∴AC⊥BD,
∵BB′⊥平面ABCD,AC?平面ABCD,
∴BB′⊥AC,
∵BB′∩DB′=B,BB′?平面DBB′,AC?平面DBB′,
∴AC⊥平面DBB′,
∵DB′?平面DBB′,
∴AC⊥DB′,
∵MN∥AC,
∴DB′⊥MN,
同理可证DB′⊥MF,DB′⊥NF,
∵MF∩NF=F,MF?平面MNF,NF?平面MNF,
∴DB′⊥平面MNF,即I垂直于平面MNP,故①正确.
④中由①中证明可知I⊥MP,
∵MN∥AC,
AC⊥I,
∴I⊥MN,
∴I⊥平面MNP,
同理可证明⑤中I⊥平面MNP.
故答案为:①④⑤
点评:本题主要考查了线面垂直的判定定理.考查了学生空间思维能力和观察能力.

练习册系列答案
相关题目
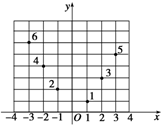 如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项,如下表所示.
如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项,如下表所示.