题目内容
已知函数f（x）=2cos（x-
），x∈R．
（Ⅰ）求f（-
）的值；
（Ⅱ）若cos（θ+
）=
，θ∈（-
，
），求f（2θ+
）．
| π |
| 12 |
（Ⅰ）求f（-
| π |
| 6 |
（Ⅱ）若cos（θ+
| π |
| 3 |
| 3 |
| 5 |
| π |
| 2 |
| π |
| 2 |
| π |
| 12 |
考点：二倍角的余弦,二倍角的正弦
专题：三角函数的求值
分析：（I）根据函数f（x）的解析式，即可求得f（-
）的值．
（II）根据θ∈（-
，
）及cos（θ+
）=
，求得sin（θ+
）=
．再利用二倍角公式求得 cos2（θ+
）和sin2（θ+
）的值．再由 f（2θ+
）=2cos2θ=2cos[2（θ+
）-
]，利用两角差的余弦公式计算求得结果．
| π |
| 6 |
（II）根据θ∈（-
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| 3 |
| 5 |
| π |
| 3 |
| 4 |
| 5 |
| π |
| 3 |
| π |
| 3 |
| π |
| 12 |
| π |
| 3 |
| 2π |
| 3 |
解答：
解：（I）∵函数f（x）=2cos（x-
），∴f（-
）=2cos（-
-
）=2cos（-
）=cos
=
．
（II）∵θ∈（-
，
），∴-
＜θ+
＜
．
∵cos（θ+
）=
∈（
，
）∴
＜θ+
＜
，∴sin（θ+
）=
．
∴cos2（θ+
）=2cos2(θ+
)-1=-
，sin2（θ+
）=2sin（θ+
）cos（θ+
）=
．
∴f（2θ+
）=2cos（2θ+
-
）=2cos2θ=2cos[2（θ+
）-
]=2cos2（θ+
）cos
+2sin2（θ+
）sin
=2×（-
）×（-
）+2
×
=
．
| π |
| 12 |
| π |
| 6 |
| π |
| 6 |
| π |
| 12 |
| π |
| 4 |
| π |
| 4 |
| 2 |
（II）∵θ∈（-
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
∵cos（θ+
| π |
| 3 |
| 3 |
| 5 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 4 |
| 5 |
∴cos2（θ+
| π |
| 3 |
| π |
| 3 |
| 7 |
| 25 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 24 |
| 25 |
∴f（2θ+
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
=2×（-
| 7 |
| 25 |
| 1 |
| 2 |
| 24 |
| 25 |
| ||
| 2 |
7+24
| ||
| 25 |
点评：本题主要考查同角三角函数的基本关系、诱导公式、二倍角公式的应用，属于中档题．
练习册系列答案
相关题目
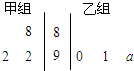如图所示茎叶图记录了甲、乙两组各三名同学在期末考试的数学成绩，乙组记录中有一个数字模糊，无法确认．假设这个数字具有随机性，并在图中以a表示．
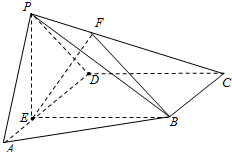如图，在四棱锥P-ABCD中，E为AD上一点，PE⊥平面ABCD．AD∥BC，AD⊥CD，BC=ED=2AE=2，EB=3，F为PC上一点，且CF=2FP．