题目内容
已知正三棱柱底面边长是2,外接球的表面积是16π,则该三棱柱的侧棱长 .
考点:球内接多面体
专题:计算题,空间位置关系与距离
分析:根据三棱柱外接球的表面积是16π,求出该球的半径R=2,根据正三棱柱底面边长是2,可得底面三角形的外接圆半径,从而可求三棱柱的侧棱长.
解答:
 解:∵该三棱柱外接球的表面积是16π,
解:∵该三棱柱外接球的表面积是16π,
∴4πR2=16π,
∴该球的半径R=2,
又正三棱柱底面边长是2,
∴底面三角形的外接圆半径r=
=
,
∴该三棱柱的侧棱长是2
=
.
故答案为:
.
 解:∵该三棱柱外接球的表面积是16π,
解:∵该三棱柱外接球的表面积是16π,∴4πR2=16π,
∴该球的半径R=2,
又正三棱柱底面边长是2,
∴底面三角形的外接圆半径r=
| 2 |
| 3 |
| 4-1 |
2
| ||
| 3 |
∴该三棱柱的侧棱长是2
22-(
|
4
| ||
| 3 |
故答案为:
4
| ||
| 3 |
点评:本题主要考查空间几何体中位置关系、球和正棱柱的性质以及相应的运算能力和空间形象能力.

练习册系列答案
相关题目
运行如图所示的程序框图后输出的结果是( )


| A、14 | B、16 | C、18 | D、64 |
执行如图的程序框图输出的T的值为( )


| A、4 | B、6 | C、8 | D、10 |
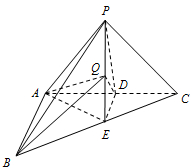 如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC,D,E分别是AC,BC的中点,AB=2
如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC,D,E分别是AC,BC的中点,AB=2