题目内容
已知在△ABC中,∠A,
∠B,∠C成等差数列,最大边长为x,最小边长为1
(Ⅰ)求sinA+sinC的最大值;
(Ⅱ)用λ(x)表示△ABC的周长与面积的比,求λ(x)的值域.
| 1 |
| 2 |
(Ⅰ)求sinA+sinC的最大值;
(Ⅱ)用λ(x)表示△ABC的周长与面积的比,求λ(x)的值域.
考点:等差数列的性质
专题:解三角形
分析:(Ⅰ)由等差中项的性质和内角和定理求出B,再由诱导公式和两角和的正弦公式化简sinA+sinC,利用角的范围和正弦函数的性质,求出式子的最大值;
(Ⅱ)由题意求出三角形的第三边,求出λ(x)的表达式,利用分离常数法求出λ(x)的值域.
(Ⅱ)由题意求出三角形的第三边,求出λ(x)的表达式,利用分离常数法求出λ(x)的值域.
解答:
解:(Ⅰ)因为∠A,
∠B,∠C成等差数列,
所以2×
∠B=∠A+∠C,则∠B=∠A+∠C,
又∠A+∠B+∠C=π,所以∠B=
,
则sinA+sinC=sinA+sin(
-A)=sinA+cosA=
sin(A+
),
因为0<A<
,所以
<A+
<
,
当A+
=
时,即A=
,sinA+sinC取到最大值是
;
(Ⅱ)因为∠B=
,且最大边长为x,最小边长为1,
所以另外一条直角边为
(x>1),
则λ(x)=
=2(
)=2(1+
)
=2(1+
)=2(1+
)=2(1+
)>4,
所以λ(x)的值域是(4,+∞).
| 1 |
| 2 |
所以2×
| 1 |
| 2 |
又∠A+∠B+∠C=π,所以∠B=
| π |
| 2 |
则sinA+sinC=sinA+sin(
| π |
| 2 |
| 2 |
| π |
| 4 |
因为0<A<
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
当A+
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 2 |
(Ⅱ)因为∠B=
| π |
| 2 |
所以另外一条直角边为
| x2-1 |
则λ(x)=
1+x+
| ||||
|
1+x+
| ||
|
| 1+x | ||
|
=2(1+
|
|
1+
|
所以λ(x)的值域是(4,+∞).
点评:本题考查等差中项的性质,内角和定理,诱导公式和两角和的正弦公式,以及正弦函数的性质,考查分离常数法化简函数解析式,比较综合.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
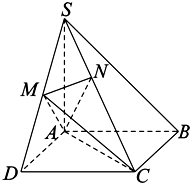 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB,点M是SD的中点,AN⊥SC,且交SC于点N.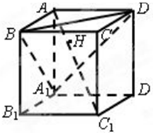 如图,正方体AC1的棱长为1,连结AC1,交平面A1BD于H,有以下四个命题:
如图,正方体AC1的棱长为1,连结AC1,交平面A1BD于H,有以下四个命题:



