题目内容
10．已知向量$\overrightarrow{a}$=（1，-2），$\overrightarrow{b}$=（1，1），$\overrightarrow{m}$=$\overrightarrow{a}$+$\overrightarrow{b}$，$\overrightarrow{n}$=$\overrightarrow{a}$-λ$\overrightarrow{b}$，如果$\overrightarrow{m}$⊥$\overrightarrow{n}$，那么实数λ=（ ）| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
分析 由平面向量坐标运算法则先分别求出$\overrightarrow{m}，\overrightarrow{n}$，再由$\overrightarrow{m}$⊥$\overrightarrow{n}$，能求出实数λ．
解答 解：∵量$\overrightarrow{a}$=（1，-2），$\overrightarrow{b}$=（1，1），
∴$\overrightarrow{m}$=$\overrightarrow{a}$+$\overrightarrow{b}$=（2，-1），
$\overrightarrow{n}$=$\overrightarrow{a}$-λ$\overrightarrow{b}$=（1-λ，-2-λ），
∵$\overrightarrow{m}$⊥$\overrightarrow{n}$，∴$\overrightarrow{m}•\overrightarrow{n}$=2（1-λ）+（-1）（-2-λ）=0，
解得实数λ=4．
故选：A．
点评 本题考查实数值的求法，涉及到平面向量坐标运算法则、向量垂直的性质的应用等基础知识，考查推理论证能力、运算求解能力，考查函数与方程思想，是基础题．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
20．
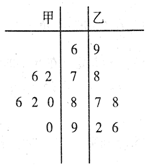甲、乙两名学生的六次数学测试成绩（百分制）如图所示．
①甲同学成绩的中位数大于乙同学成绩的中位数；
②甲同学的平均分比乙同学高；
③甲同学的平均分比乙同学低；
④甲同学成绩的标准差小于乙同学成绩的标准差．
上面说法正确的是（ ）
甲、乙两名学生的六次数学测试成绩（百分制）如图所示．①甲同学成绩的中位数大于乙同学成绩的中位数；
②甲同学的平均分比乙同学高；
③甲同学的平均分比乙同学低；
④甲同学成绩的标准差小于乙同学成绩的标准差．
上面说法正确的是（ ）
| A． | ③④ | B． | ①② | C． | ②④ | D． | ①③④ |
1．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的一条渐近线方程为$y=\frac{3}{4}x$，则双曲线的离心率为（ ）
| A． | $\frac{5}{3}$ | B． | $\frac{{\sqrt{21}}}{3}$ | C． | $\frac{5}{4}$ | D． | $\frac{{\sqrt{7}}}{2}$ |
中，茎2的叶子数为3．
2．双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的渐近线为等边三角形OAB的边OA、OB所在直线，直线AB过焦点，且|AB|=2，则双曲线实轴长为（ ）
| A． | $\sqrt{3}$ | B． | $3\sqrt{2}$ | C． | $\frac{3}{2}$ | D． | 3 |
19．已知函数f（x）=sin（2x-$\frac{π}{3}$），g（x）=x2-2，若对任意的实数x1，总存在实数x2使得f（x1）=g（x2）成立，则x2的取值范围是（ ）
| A． | [-1，1] | B． | $[{-\sqrt{3}，\sqrt{3}}]$ | C． | （-∞，-1]∪[1，+∞） | D． | [-$\sqrt{3}$，-1]∪[1，$\sqrt{3}$] |
6．
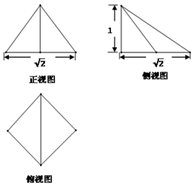如图是一个简单几何体的三视图，则该几何体的体积为（ ）
如图是一个简单几何体的三视图，则该几何体的体积为（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | 1 |