题目内容
19.已知函数f(x)=sin(2x-$\frac{π}{3}$),g(x)=x2-2,若对任意的实数x1,总存在实数x2使得f(x1)=g(x2)成立,则x2的取值范围是( )| A. | [-1,1] | B. | $[{-\sqrt{3},\sqrt{3}}]$ | C. | (-∞,-1]∪[1,+∞) | D. | [-$\sqrt{3}$,-1]∪[1,$\sqrt{3}$] |
分析 由题意,求出f(x)的值域,根据对任意的实数x1,总存在实数x2使得f(x1)=g(x2)成立,可得g(x)的值域,即可求出x2的取值范围.
解答 解:函数f(x)=sin(2x-$\frac{π}{3}$),
根据正弦函数性可知:f(x)的值域为[-1,1],
对任意的实数x1,总存在实数x2使得f(x1)=g(x2)成立,
∴[-1,1]⊆g(x).
∵g(x)=x2-2,
根据二次函数性质可知:当g(x)=-1时,可得x=±1,
当g(x)=1时,可得x=±$\sqrt{3}$,
由二洗函数的图象可得:[-$\sqrt{3}$,-1]∪[1,$\sqrt{3}$].
故选:D.
点评 本题考查了三角函数性质以及二次函数的图象及性质的运用,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
9.抛物线y2=2px的焦点为F,点A、B、C在此抛物线上,点A坐标为(1,2).若点F恰为△ABC的重心,则直线BC的方程为( )
| A. | x+y=0 | B. | 2x+y-1=0 | C. | x-y=0 | D. | 2x-y-1=0 |
7.设全集U=R,集合A={y|y=3-x2},B={x|y=log2(x+2)},则(∁UA)∩B=( )
| A. | {x|-2<x≤3} | B. | {x|x>3} | C. | {x|x≥3} | D. | {x|x<-2} |
11.若偶函数f(x)在(-∞,0]上单调递减,a=log2$\frac{1}{3}$,b=log4$\frac{1}{5}$,c=${2^{\frac{3}{2}}}$,则f(a),f(b),f(c)满足( )
| A. | f(a)<f(b)<f(c) | B. | f(b)<f(a)<f(c) | C. | f(c)<f(a)<f(b) | D. | f(c)<f(b)<f(a) |
14.已知等比数列{an}的前n项和为Sn,若S3、S9、S6成等差数列,则下列说法错误的是( )
| A. | a3、a6、a9成等比数列 | B. | a3、a6、a9成等差数列 | ||
| C. | S2、S8、S5成等比数列 | D. | S2、S8、S5成等差数列 |
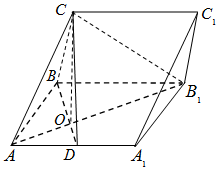 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2$\sqrt{2}$,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.