题目内容
20．
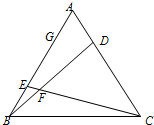如图，正△ABC中，点D在边AC上，E，G在边AB上，且AB=3AG=6，AD=λAC，AE=（1-λ）AB，（0＜λ＜1），BD，CE相交于点F（1）证明：A，E，F，D四点共圆；
（2）当点E是BG中点时，求线段FG的长度．
分析 （1）先证明△BCE≌△ABD，得到∠BEC=∠ADB，再利用对角互补四点共圆，即可证明；
（2）证明以AE为直径的圆圆心为G，即可求线段FG的长度．
解答 （1）证明：∵AE=（1-λ）AB，∴BE=λAB．
∵AD=λAC，∴BE=AD，
又∠CBE=∠BAD，CB=BA，
∴△BCE≌△ABD，∴∠BEC=∠ADB，
∴∠ADB+∠AEC=180°，∴A，E，F，D四点共圆； …（4分）
（2）解：连接DE，GF，
∵BE=AD=2，AE=4，A=60°，∴AD⊥DE，
∴以AE为直径的圆圆心为G，∴$GF=\frac{1}{2}AE=2$…（6分）
点评 本题考查对角互补四点共圆，考查圆的直径的性质，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
19．偶函数f（x）在[0，+∞）上单调递增，若f（1）=0，则不等式f（x）＞0的解集是（ ）
| A． | （-1，0）∪（0，1） | B． | （-∞，-1）∪（1，+∞） | C． | （-∞，-1）∪（0，1） | D． | （-1，0）∪（1，+∞） |
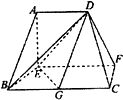在如图所示的多面体中，底面BCFE是梯形，EF∥BC，EF⊥EB，又平面ABE⊥平面BCFE，AD∥EF，BC=2AD=4，EF=3，AE=BE=2，AB=2$\sqrt{2}$．
在如图所示的几何体中，四边形ABCD是正方形，EA⊥底面ABCD，EF∥AD，且AB=6，AE=3$\sqrt{2}$，EF=3．
如图，在四棱锥S-ABCD中，底面ABCD是正方形，SA⊥底面ABCD，SA=AB=1，点M是SD的重点，AN⊥SC，且交SC于点N．