题目内容
13.已知函数f(x)=2-$\frac{ax+2}{{e}^{x}}$(a∈R)(1)讨论函数f(x)的单调性;
(2)当x≥0时,f(x)≥0,求a的取值范围.
分析 (1)先求出函数的导函数,再分类讨论即可求出函数的单调区间,
(2)根据函数的单调性和最值得关系分类讨论即可求出参数m的取值范围.
解答 解:(1)函数f(x)的定义域为R,
则f′(x)=-$\frac{ax-a+2}{{e}^{x}}$,
若a>0,令f′(x)<0,解得x<$\frac{a-2}{a}$,令f′(x)>0,解得x>$\frac{a-2}{a}$,
∴f(x)在(-∞,$\frac{a-2}{a}$)上单调递减,在($\frac{a-2}{a}$,+∞)单调递增,
若a<0,令f′(x)>0,解得x<$\frac{a-2}{a}$,令f′(x)>0,解得x>$\frac{a-2}{a}$,
∴f(x)在(-∞,$\frac{a-2}{a}$)上单调递增,在($\frac{a-2}{a}$,+∞)单调递减,
若a=0,f′(x)=$\frac{2}{{e}^{x}}$>0,
∴f(x)在R上单调递增;
(2)注意到f(0)=0,即当x≥0时,f(x)≥f(0),
①当a>0时,f(x)在(-∞,$\frac{a-2}{a}$)上单调递减,关故由f(x)≥f(0)可得$\frac{a-2}{a}$≤0,解得0<a≤2,
②当a<0时,$\frac{a-2}{a}$>0,由于f(x)在[0,$\frac{a-2}{a}$)上单调递增,在($\frac{a-2}{a}$,+∞)单调递减,
当0<x<$\frac{a-2}{a}$时,f(x)>f(0)=0,
当x>$\frac{a-2}{a}$时,-ax-2>-a>0,
f(x)=2-$\frac{ax+2}{{e}^{x}}$=2+$\frac{-ax-2}{{e}^{x}}$>2,
故有f(x)>0,
③当a=0时,f(x)在R上单调递增,
∴f(x)≥f(0)恒成立,
综上所述a的取值范围为(-∞,2]
点评 本题考查导数的运用,求单调区间和最值,考查运算能力,分类讨论的思想,属于中档题.

| A. | {1,2,3} | B. | {1,3} | C. | {1,2} | D. | {1} |
| A. | a>b>2 | B. | a>3,-3<b<-1 | ||
| C. | a<0<b,a+b>0 | D. | a>2,-2<b<0,a-b>4 |
| A. | 4 | B. | $\frac{25}{3}$ | C. | -89 | D. | $\frac{17}{3}$ |
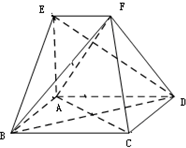 在如图所示的几何体中,四边形ABCD是正方形,EA⊥底面ABCD,EF∥AD,且AB=6,AE=3$\sqrt{2}$,EF=3.
在如图所示的几何体中,四边形ABCD是正方形,EA⊥底面ABCD,EF∥AD,且AB=6,AE=3$\sqrt{2}$,EF=3. 如图,平面ABCD⊥平面ABE,其中ABCD为矩形,△ABE为直角三角形,∠AEB=90°,AB=2AD=2AE=2.
如图,平面ABCD⊥平面ABE,其中ABCD为矩形,△ABE为直角三角形,∠AEB=90°,AB=2AD=2AE=2.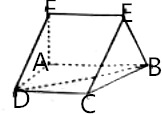 如图,在直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=CD=$\frac{1}{2}$AB=1,直角梯形ABEF可以通过直角梯形ABCD以直线AB为轴旋转得到,且平面ABEF⊥平面ABCD
如图,在直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=CD=$\frac{1}{2}$AB=1,直角梯形ABEF可以通过直角梯形ABCD以直线AB为轴旋转得到,且平面ABEF⊥平面ABCD