题目内容
1．已知函数f（x）=2sin x，对任意的x∈R都有f（x1）≤f（x）≤f（x2），则|x1-x2|的最小值为（ ）| A． | $\frac{π}{4}$ | B． | $\frac{π}{2}$ | C． | π | D． | 2π |
分析 根据正弦函数的图象及性质可知函数f（x）=2sin x的周期为2π，任意的x∈R都有f（x1）≤f（x）≤f（x2），
则|x1-x2|的最小值为π．可得答案．
解答 解：函数f（x）=2sin x，
由正弦函数的图象及性质：可得f（x）=2sin x的周期为2π，
∴|x1-x2|的最小值为π．
故选C．
点评 本题考查了正弦型三角函数的图象即性质的运用，属于基础题．
练习册系列答案
小题狂做系列答案
相关题目
14．已知集合A={-1，0，1}，B={y|y=πx，x∈A}，则A∩B=（ ）
| A． | {-1} | B． | {0} | C． | {1} | D． | {0，1} |
9．在对一种新药进行药效评估时，调查了20位开始使用这种药的人，结果有16人认为新药比常用药更有效，则（ ）
| A． | 该新药的有效率为80% | |
| B． | 该新药比常用药更有效 | |
| C． | 该新药为无效药 | |
| D． | 本试验需改进，故不能得出新药比常用药更有效的结论 |
16．满足f（x）=f'（x）的一个函数是（ ）
| A． | f（x）=1-x | B． | f（x）=x | C． | f（x）=ex | D． | f（x）=1 |
6．复平面内，若复数z=a2（1+i）-a（4+i）-6i所对应的点在第二象限，则实数a的取值范围是（ ）
| A． | （0，3） | B． | （3，4） | C． | （-2，0） | D． | （-∞，-2） |
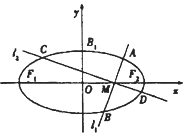设椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的两个焦点为F1，F2，点B1为其短轴的一个端点，满足$|{\overrightarrow{{B_1}{F_1}}+\overrightarrow{{B_1}{F_2}}}|=2|{\overrightarrow{{B_1}{F_1}}}|+|{\overrightarrow{{B_1}{F_2}}}|=2，\overrightarrow{{B_1}{F_1}}•\overrightarrow{{B_1}{F_2}}$=-2．