Question

8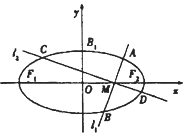．设椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的两个焦点为F₁，F₂，点B₁为其短轴的一个端点，满足$|{\overrightarrow{{B_1}{F_1}}+\overrightarrow{{B_1}{F_2}}}|=2|{\overrightarrow{{B_1}{F_1}}}|+|{\overrightarrow{{B_1}{F_2}}}|=2，\overrightarrow{{B_1}{F_1}}•\overrightarrow{{B_1}{F_2}}$=-2．
（1）求椭圆C的方程；
（2）过点M（1，0）作两条互相垂直的直线l₁，l₂，设l₁与椭圆交于点A，B，与椭圆交于C，D，求$\overrightarrow{AC}•\overrightarrow{DB}$的最小值．

Answer 1

分析 （1）由向量的加法可知丨$\overrightarrow{{B}_{1}{F}_{1}}$+$\overrightarrow{{B}_{1}{F}_{2}}$丨=2b=2，则b=1，则$\overrightarrow{{B}_{1}{F}_{1}}$•$\overrightarrow{{B}_{1}{F}_{2}}$=-c²+b²=-2，求得c，则a²=b²+c²=4，即可求得椭圆方程；
（2）分类，直线l₁与x轴重合时，求得A，B，C和D点坐标，即可求得$\overrightarrow{AC}•\overrightarrow{DB}$的值，当直线直线l₁不与x轴重合时，设直线方程，代入椭圆方程，利用韦达定理，向量数量积的坐标运算$\overrightarrow{AC}•\overrightarrow{DB}$=-$\overrightarrow{MC}$•$\overrightarrow{MD}$-$\overrightarrow{MA}$•$\overrightarrow{MB}$，利用基本不等式的性质即可求得$\overrightarrow{AC}•\overrightarrow{DB}$的最小值．

解答 解：（1）不妨设F₁（-c，0），F₂（c，0），B₁（0，b），
则丨$\overrightarrow{{B}_{1}{F}_{1}}$+$\overrightarrow{{B}_{1}{F}_{2}}$丨=2b=2，b=1，
则$\overrightarrow{{B}_{1}{F}_{1}}$•$\overrightarrow{{B}_{1}{F}_{2}}$=-c²+b²=-2，则c=$\sqrt{3}$，
a²=b²+c²=4，
∴椭圆C的方程$\frac{{x}^{2}}{4}+{y}^{2}=1$；
（2）当直线l₁与x轴重合时，则A（-2，0），B（2，0），C（1，$\frac{\sqrt{3}}{2}$），D（1，-$\frac{\sqrt{3}}{2}$），
则$\overrightarrow{AC}•\overrightarrow{DB}$=3×1×$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{15}{4}$，
当直线直线l₁不与x轴重合时，设直线x=my+1，A（x₁，y₁），B（x₂，y₂），
∴$\left\{\begin{array}{l}{x=my+1}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$，整理得：（m²+4）y²+2my-3=0，
∴y₁+y₂=-$\frac{2m}{{m}^{2}+4}$，y₁y₂=$\frac{3（{m}^{2}+1）}{{m}^{2}+4}$，
$\overrightarrow{AC}•\overrightarrow{DB}$=（$\overrightarrow{MC}$-$\overrightarrow{MA}$）（$\overrightarrow{MB}$-$\overrightarrow{MD}$）=-$\overrightarrow{MC}$•$\overrightarrow{MD}$-$\overrightarrow{MA}$•$\overrightarrow{MB}$，
$\overrightarrow{MA}$=（x₁-1，y₁）=（my₁，y₁），$\overrightarrow{MB}$=（x₂-1，y₂）=（my₂，y₂），
-$\overrightarrow{MA}$•$\overrightarrow{MB}$=-（m²+1）y₁y₂=$\frac{3（{m}^{2}+1）}{{m}^{2}+4}$，
由直线l₁与直线l₂相互垂直，则-$\overrightarrow{MC}$•$\overrightarrow{MD}$=$\frac{3（1+{m}^{2}）}{1+4{m}^{2}}$，
则$\overrightarrow{AC}•\overrightarrow{DB}$=-$\overrightarrow{MC}$•$\overrightarrow{MD}$-$\overrightarrow{MA}$•$\overrightarrow{MB}$，
=$\frac{3（1+{m}^{2}）}{1+4{m}^{2}}$+$\frac{3（{m}^{2}+1）}{{m}^{2}+4}$=$\frac{15（{m}^{2}+1）^{2}}{（{m}^{2}+4）（1+4{m}^{2}）}$≥$\frac{15（{m}^{2}+1）^{2}}{（\frac{5{m}^{2}+5}{2}）^{2}}$=$\frac{12}{5}$，
当且仅当m=±1时，取“=”，
∴$\overrightarrow{AC}•\overrightarrow{DB}$的最小值$\frac{12}{5}$．

点评 本题考查椭圆的标准方程及性质，考查直线与椭圆的位置关系，韦达定理，向量坐标运算，考查计算能力，属于中档题．